Two-ray ground-reflection model

2-ray Ground Reflected Model is a radio propagation model that predicts path loss when the signal received consists of the line of sight component and multi path component formed predominately by a single ground reflected wave.

2-Ray Ground Reflection diagram including variables for the 2-ray ground reflection propagation algorithm.

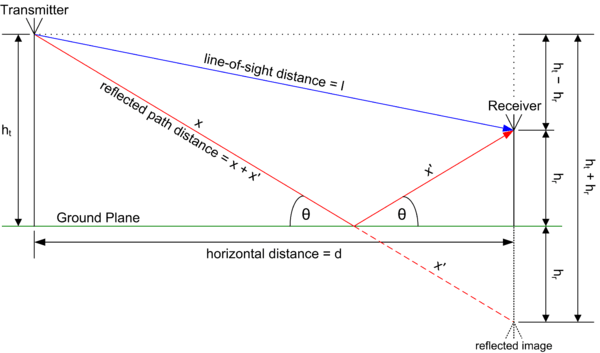
Mathematical Derivation

From the figure the received line of sight component may be written as

$r_{{los}}(t)=Re\left\{{\frac {\lambda {\sqrt {G_{{los}}}}}{4\pi }}\times {\frac {s(t)e^{{-j2\pi l/\lambda }}}{l}}\right\}$

and the ground reflected component may be written as

$r_{{gr}}(t)=Re\left\{{\frac {\lambda \Gamma (\theta ){\sqrt {G_{{gr}}}}}{4\pi }}\times {\frac {s(t-\tau )e^{{-j2\pi (x+x')/\lambda }}}{x+x'}}\right\}$

where $s(t)$ is the transmitted signal, $l$ is the length of the direct line-of-sight (LOS) ray, ${\displaystyle x+x'}$ is the length of the ground-reflected ray, ${\displaystyle G_{los}}$ is the combined antenna gain along the LOS path, ${\displaystyle G_{gr}}$ is the combined antenna gain along the ground-reflected path, $\lambda$ is the wavelength of the transmission ($\lambda ={\frac {c}{f}}$, where $c$ is the speed of light and $f$ is the transmission frequency), $\Gamma (\theta )$ is ground reflection co-efficient and $\tau$ is the delay spread of the model which equals $(x+x'-l)/c$

Ground Reflection $\Gamma (\theta )={\frac {\sin \theta -X}{\sin \theta +X}}$

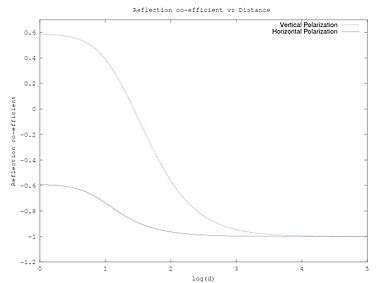
where $X$ for vertical polarization is ${\displaystyle X_{v}={\frac {\sqrt {\varepsilon _{g}-{\cos }^{2}\theta }}{\varepsilon _{g}}}}$

and for horizontal polarization is $X_{{h}}={\sqrt {\varepsilon _{{g}}-{\cos }^{2}\theta }}$,

${\displaystyle \varepsilon _{g}}$ is the relative permittivity of the ground and $\theta$ is the angle between the ground and the reflected ray.

From the figure

$x+x'={\sqrt {(h_{t}+h_{r})^{2}+d^{2}}}$

and

$l={\sqrt {(h_{t}-h_{r})^{2}+d^{2}}}$,

therefore, the path difference between them

$\Delta d=x+x'-l={\sqrt {(h_{t}+h_{r})^{2}+d^{2}}}-{\sqrt {(h_{t}-h_{r})^{2}+d^{2}}}$

and the phase difference between the waves is

$\Delta \phi ={\frac {2\pi \Delta d}{\lambda }}$

The power of the signal received is

$r_{{los}}^{2}+r_{{gr}}^{2}$

If the signal is narrow band relative to the delay spread $\tau$, the power equation $s(t)=s(t-\tau )$ may be simplified to

$|s(t)|^{2}\left({{\frac {\lambda }{4\pi }}}\right)^{2}\times \left({\frac {{\sqrt {G_{{los}}}}\times e^{{-j2\pi l/\lambda }}}{l}}+\Gamma (\theta ){\sqrt {G_{{gr}}}}{\frac {e^{{-j2\pi (x+x')/\lambda }}}{x+x'}}\right)^{2}=P_{t}\left({{\frac {\lambda }{4\pi }}}\right)^{2}\times \left({\frac {{\sqrt {G_{{los}}}}}{l}}+\Gamma (\theta ){\sqrt {G_{{gr}}}}{\frac {e^{{-j\Delta \phi }}}{x+x'}}\right)^{2}$

where $P_{t}$ is the transmitted power.

When distance between the antennas $d$ is very large relative to the height of the antenna we may expand $x+x'-l$ using Generalized Binomial Theorem

${\begin{aligned}x+x'-l&={\sqrt {(h_{t}+h_{r})^{2}+d^{2}}}-{\sqrt {(h_{t}-h_{r})^{2}+d^{2}}}\\&=d{\Bigg (}{\sqrt {{\frac {(h_{t}+h_{r})^{2}}{d^{2}}}+1}}-{\sqrt {{\frac {(h_{t}-h_{r})^{2}}{d^{2}}}+1}}{\Bigg )}\\\end{aligned}}$

Using the Taylor series of ${\sqrt {1+x}}$:

$\sqrt{1 + x} = \sum_{n=0}^\infty \frac{(-1)^n(2n)!}{(1-2n)(n!)^2(4^n)}x^n = 1 + \textstyle \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16} x^3 - \frac{5}{128} x^4 + \dots,\!$

and taking the first two terms

$x+x'-l\approx {\frac {d}{2}}\times \left({\frac {(h_{t}+h_{r})^{2}}{d^{2}}}-{\frac {(h_{t}-h_{r})^{2}}{d^{2}}}\right)={\frac {2h_{t}h_{r}}{d}}$

Phase difference may be approximated as

$\Delta \phi \approx {\frac {4\pi h_{t}h_{r}}{\lambda d}}$

When $d$ increases asymptotically

Reflection co-efficient tends to -1 for large d.

${\begin{aligned}d&\approx l\approx x+x',\\\Gamma (\theta )&\approx -1,\\G_{{los}}&\approx G_{{gr}}=G\\\end{aligned}}$

$\therefore P_{r}=P_{t}\left({{\frac {\lambda {\sqrt {G}}}{4\pi d}}}\right)^{2}\times (1-e^{{-j\Delta \phi }})^{2}$

Expanding $e^{{-j\Delta \phi }}$using Taylor series

$e^{x}=1+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots =1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots \!=\sum _{{n=0}}^{\infty }{\frac {x^{n}}{n!}}$

and retaining only the first two terms

${\displaystyle e^{-j\Delta \phi }\approx 1+({-j\Delta \phi })+\cdots =1-j\Delta \phi }$

${\begin{aligned}\therefore P_{r}&\approx P_{t}\left({{\frac {\lambda {\sqrt {G}}}{4\pi d}}}\right)^{2}\times (1-(1-j\Delta \phi ))^{2}\\&=P_{t}\left({{\frac {\lambda {\sqrt {G}}}{4\pi d}}}\right)^{2}\times (j\Delta \phi )^{2}\\&=P_{t}\left({{\frac {\lambda {\sqrt {G}}}{4\pi d}}}\right)^{2}\times -\left({\frac {4\pi h_{t}h_{r}}{\lambda d}}\right)^{2}\\&=-P_{t}{\frac {Gh_{t}^{2}h_{r}^{2}}{d^{4}}}\end{aligned}}$

Taking the magnitude

$|P_{r}|=P_{t}{\frac {Gh_{t}^{2}h_{r}^{2}}{d^{4}}}$

Power varies with inverse fourth power of distance for large $d$.

In logarithmic units

In logarithmic units : $P_{{r_{{dBm}}}}=P_{{t_{{dBm}}}}+10\log _{{10}}(Gh_{t}^{2}h_{r}^{2})-40\log _{{10}}(d)$

Path loss : $PL\;=P_{{t_{{dBm}}}}-P_{{r_{{dBm}}}}\;=40\log _{{10}}(d)-10\log _{{10}}(Gh_{t}^{2}h_{r}^{2})$

Power vs. Distance Characteristics

Power vs distance plot

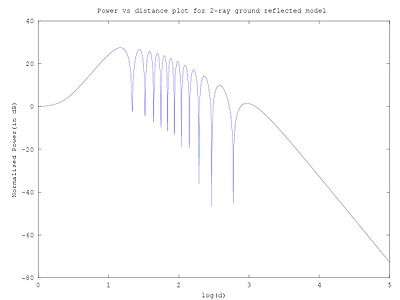
When d is small compared to transmitter height two waves add constructively to yield higher power and as d increases these waves add up constructively and destructively giving regions of up-fade and down-fade as d increases beyond the critical distance or first Fresnel zone power drops proportional to inverse fourth power of d. An approximation to critical distance may be obtained by setting Δφ to π as critical distance a local maximum.

As a case of log distance path loss model

The standard expression of Log distance path loss model is

$PL\;=P_{{T_{{dBm}}}}-P_{{R_{{dBm}}}}\;=\;PL_{0}\;+\;10\gamma \;\log _{{10}}{\frac {d}{d_{0}}}\;+\;X_{g},$

The path loss of 2-ray ground reflected wave is

$PL\;=P_{{t_{{dBm}}}}-P_{{r_{{dBm}}}}\;=40\log _{{10}}(d)-10\log _{{10}}(Gh_{t}^{2}h_{r}^{2})$

where

$PL_{0}=40\log _{{10}}(d_{0})-10\log _{{10}}(Gh_{t}^{2}h_{r}^{2})$,

$X_{g}=0$

and

$\gamma =4$

for $d,d_{0}>d_{c}$ the critical distance.

As a case of multi-slope model

The 2-ray ground reflected model may be thought as a case of multi-slope model with break point at critical distance with slope 20 dB/decade before critical distance and slope of 40 dB/decade after the critical distance.

See also

• Radio propagation model
• Free-space path loss
• Friis transmission equation

References

Goldsmith, Andrea (2004). Wireless communications (1. publ. ed.). Cambridge, U.K.: Cambridge University Press. ISBN 978-0521837163.

Institute, organized by The Korean Institute of Communications and Information Sciences ; Electronics and Telecommunications Research. ICTC 2012 2012 International Conference on ICT Convergence : "Global Open Innovation Summit for Smart ICT Convergence," October 15-17, 2012, Ramada Plaza Jeju Hotel, Jeju Island, Korea. Piscataway, NJ: IEEE. pp. 454–455. ISBN 978-1-4673-4827-0.

Rappaport, Theodore S. (2002). Wireless communications : principles and practice (2. ed.). Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0130422323.