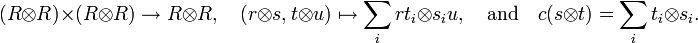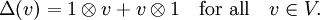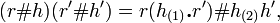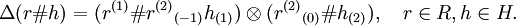Braided Hopf algebra
In mathematics, a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfeld category of a Hopf algebra H, particularly the Nichols algebra of a braided vectorspace in that category.
The notion should not be confused with quasitriangular Hopf algebra.
Definition
Let H be a Hopf algebra over a field k, and assume that the antipode of H is bijective. A Yetter–Drinfeld module R over H is called a braided bialgebra in the Yetter–Drinfeld category 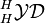 if
if
-
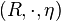 is a unital associative algebra, where the multiplication map
is a unital associative algebra, where the multiplication map 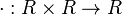 and the unit
and the unit 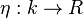 are maps of Yetter–Drinfeld modules,
are maps of Yetter–Drinfeld modules, -
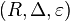 is a coassociative coalgebra with counit
is a coassociative coalgebra with counit  , and both
, and both 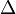 and
and  are maps of Yetter–Drinfeld modules,
are maps of Yetter–Drinfeld modules, - the maps
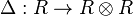 and
and 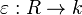 are algebra maps in the category
are algebra maps in the category 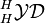 , where the algebra structure of
, where the algebra structure of 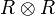 is determined by the unit
is determined by the unit 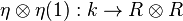 and the multiplication map
and the multiplication map
-
- Here c is the canonical braiding in the Yetter–Drinfeld category
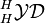 .
.
A braided bialgebra in 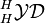 is called a braided Hopf algebra, if there is a morphism
is called a braided Hopf algebra, if there is a morphism 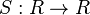 of Yetter–Drinfeld modules such that
of Yetter–Drinfeld modules such that
-
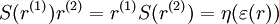 for all
for all 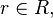
-
where 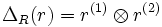 in slightly modified Sweedler notation – a change of notation is performed in order to avoid confusion in Radford's biproduct below.
in slightly modified Sweedler notation – a change of notation is performed in order to avoid confusion in Radford's biproduct below.
Examples
- Any Hopf algebra is also a braided Hopf algebra over
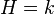
- A super Hopf algebra is nothing but a braided Hopf algebra over the group algebra
![H=k[\mathbb{Z}/2\mathbb{Z}]](../I/m/05914446e1643754653fbe1db663e8dd.png) .
. - The tensor algebra
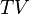 of a Yetter–Drinfeld module
of a Yetter–Drinfeld module 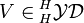 is always a braided Hopf algebra. The coproduct
is always a braided Hopf algebra. The coproduct 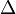 of
of 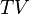 is defined in such a way that the elements of V are primitive, that is
is defined in such a way that the elements of V are primitive, that is
- The counit
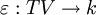 then satisfies the equation
then satisfies the equation 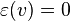 for all
for all 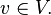
- The universal quotient of
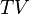 , that is still a braided Hopf algebra containing
, that is still a braided Hopf algebra containing 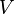 as primitive elements is called the Nichols algebra. They take the role of quantum Borel algebras in the classification of pointed Hopf algebras, analogously to the classical Lie algebra case.
as primitive elements is called the Nichols algebra. They take the role of quantum Borel algebras in the classification of pointed Hopf algebras, analogously to the classical Lie algebra case.
Radford's biproduct
For any braided Hopf algebra R in 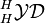 there exists a natural Hopf algebra
there exists a natural Hopf algebra  which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn Majid, who called it bosonization.
which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn Majid, who called it bosonization.
As a vector space,  is just
is just 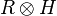 . The algebra structure of
. The algebra structure of  is given by
is given by
where  ,
, 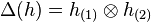 (Sweedler notation) is the coproduct of
(Sweedler notation) is the coproduct of 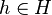 , and
, and 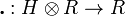 is the left action of H on R. Further, the coproduct of
is the left action of H on R. Further, the coproduct of  is determined by the formula
is determined by the formula
Here 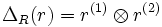 denotes the coproduct of r in R, and
denotes the coproduct of r in R, and 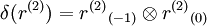 is the left coaction of H on
is the left coaction of H on 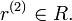
References
- Andruskiewitsch, Nicolás and Schneider, Hans-Jürgen, Pointed Hopf algebras, New directions in Hopf algebras, 1–68, Math. Sci. Res. Inst. Publ., 43, Cambridge Univ. Press, Cambridge, 2002.