Classification of Fatou components

In mathematics, Fatou components are components of the Fatou set.

Rational case

If f is a rational function

$f={\frac {P(z)}{Q(z)}}$

defined in the extended complex plane, and if it is a nonlinear function ( degree > 1 )

$\max(\deg(P),\,\deg(Q))\geq 2,$

then for a periodic component $U$ of the Fatou set, exactly one of the following holds:

1. $U$ contains an attracting periodic point
2. $U$ is parabolic^[1]
3. $U$ is a Siegel disc
4. $U$ is a Herman ring.

A Siegel disk is a simply connected Fatou component on which f(z) is analytically conjugate to a Euclidean rotation of the unit disc onto itself by an irrational rotation angle. A Herman ring is a double connected Fatou component (an annulus) on which f(z) is analytically conjugate to a Euclidean rotation of a round annulus, again by an irrational rotation angle.

Examples

• 

  Julia set (white) and Fatou set (dark red/green/blue) for $f:z\mapsto z-{\frac {g}{g'}}(z)$ with $g:z\mapsto z^{3}-1$ in the complex plane.

• 

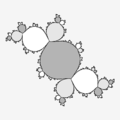
  Julia set with attracting cycle

• 

  Parabolic Julia set

• 

  Julia set with Siegel disc

• 

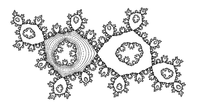
  Julia set with Herman ring

Attracting periodic point

The components of the map $f(z)=z-(z^{3}-1)/3z^{2}$ contain the attracting points that are the solutions to $z^{3}=1$. This is because the map is the one to use for finding solutions to the equation $z^{3}=1$ by Newton-Raphson formula. The solutions must naturally be attracting fixed points.

Herman ring

The map

$f(z)=e^{{2\pi it}}z^{2}(z-4)/(1-4z)\$

and t = 0.6151732... will produce a Herman ring.^[2] It is shown by Shishikura that the degree of such map must be at least 3, as in this example.

Transcendental case

Baker domain

In case of transcendental functions there is another type of periodic Fatou components, called Baker domain: these are "domains on which the iterates tend to an essential singularity (not possible for polynomials and rational functions)"^[3][4] Example function :^[5]

$f(z)=z-1+(1-2z)e^{z}$

Wandering domain

Finally, transcendental maps also may have wandering domains: these are Fatou components that are not eventually periodic.

See also

• No wandering domain theorem

References

• Lennart Carleson and Theodore W. Gamelin, Complex Dynamics, Springer 1993.
• Alan F. Beardon Iteration of Rational Functions, Springer 1991.

1. wikibooks : parabolic Julia sets
2. Milnor, John W. (1990), Dynamics in one complex variable, arXiv:math/9201272
3. An Introduction to Holomorphic Dynamics (with particular focus on transcendental functions)by L. Rempe
4. Siegel Discs in Complex Dynamics by Tarakanta Nayak
5. A transcendental family with Baker domains by Aimo Hinkkanen , Hartje Kriete and Bernd Krauskopf