Compression (functional analysis)
In functional analysis, the compression of a linear operator T on a Hilbert space to a subspace K is the operator
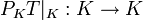 ,
,
where 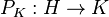 is the orthogonal projection onto K. This is a natural way to obtain an operator on K from an operator on the whole Hilbert space. If K is an invariant subspace for T, then the compression of T to K is the restricted operator K→K sending k to Tk.
is the orthogonal projection onto K. This is a natural way to obtain an operator on K from an operator on the whole Hilbert space. If K is an invariant subspace for T, then the compression of T to K is the restricted operator K→K sending k to Tk.
More generally, for a linear operator T on a Hilbert space 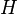 and an isometry V on a subspace
and an isometry V on a subspace 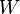 of
of 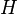 , define the compression of T to
, define the compression of T to 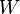 by
by
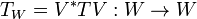 ,
,
where 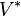 is the adjoint of V. If T is a self-adjoint operator, then the compression
is the adjoint of V. If T is a self-adjoint operator, then the compression  is also self-adjoint.
When V is replaced by the inclusion map
is also self-adjoint.
When V is replaced by the inclusion map 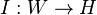 ,
, 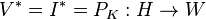 , and we acquire the special definition above.
, and we acquire the special definition above.
See also
References
- P. Halmos, A Hilbert Space Problem Book, Second Edition, Springer-Verlag, 1982.
This article is issued from Wikipedia - version of the 4/27/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.