Cross-serial dependencies

A schematic showing cross-serial dependencies. Notice that the w's and v's, which represent words, each form respective series. Notice also that the lines representing the dependency relations mutually overlap.

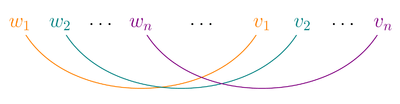
In linguistics, cross-serial dependencies (also called crossing dependencies by some authors^[1]) occur when the lines representing the dependency relations between two series of words cross over each other.^[2] They are of particular interest to linguists who wish to determine the syntactic structure of natural language; languages containing an arbitrary number of them are non-context-free. By this fact, Dutch^[3] and Swiss-German^[4] have been proved to be non-context-free.

Example

A Swiss-German sentence containing cross-serial dependencies (shown as lines between the verbs and their objects). The English translation with its dependencies, which do not cross, is shown for comparison.

A more complicated example.

As Swiss-German allows verbs and their arguments to be ordered cross-serially, we have the following example, taken from Shieber:^[4]

...mer	em Hans	s	huus	hälfed	aastriiche.
...we	Hans (dat)	the	house (acc)	help	paint.

That is, "we help Hans paint the house."

Notice that the sequential noun phrases em Hans (Hans) and s huus (the house), and the sequential verbs hälfed (help) and aastriiche (paint) both form two separate series of constituents. Notice also that the dative verb hälfed and the accusative verb aastriiche take the dative em Hans and accusative s huus as their arguments, respectively.

Why languages containing cross-serial dependencies are non-context-free

In Swiss-German sentences, the number of verbs of a grammatical case (dative or accusative) must match the number of objects of that case. Additionally, a sentence containing an arbitrary number of such objects is admissible (in principle). Hence, the following formal language is grammatical:

$L =\text{De Jan} \text{ s}\ddot{\mathrm{a}}\text{it} \text{ das} \text{ mer} \text{ (d'chind)}{}^m \text{ (em} \text{ Hans)}{}^n \text{ s} \text{ huus} \text{ h}\ddot{\mathrm{a}}\text{nd} \text{ wele} \text{ (laa)}{}^m \text{ (h}\ddot{\mathrm{a}}\text{lfe)}{}^n \text{ aastriiche.}$

It can be seen that $L$ is of the form $x a^m b^n y c^m d^n z$. By taking another image to remove the $x$, $y$ and $z$, the non-context-free^[5] language $L' = a^m b^n c^m d^n$ may be observed. All spoken languages which contain cross-serial dependencies also contain a language of a form similar to $L'$.^[2]

Treatment

Research in mildly context-sensitive language has attempted to identify a narrower and more computationally tractable subclass of context-sensitive languages that can capture context sensitivity as found in natural languages. For example cross-serial dependencies can be expressed in linear context-free rewriting systems (LCFRS); one can write a LCFRS grammar for {aⁿbⁿcⁿdⁿ | n ≥ 1} for example.^[6][7][8]

References

1. Stabler, Edward (2004), "Varieties of crossing dependencies: structure dependence and mild context sensitivity" (PDF), Cognitive Science, 28: 699–720, doi:10.1016/j.cogsci.2004.05.002.
2. Jurafsky, Daniel; Martin, James H. (2000). Speech and Language Processing (1st ed.). Prentice Hall. pp. 473–495. ISBN 978-0-13-095069-7..
3. Bresnan, Joan; M. Kaplan, Ronald (1982), "Cross-serial dependencies in Dutch", Linguistic Inquiry, 13 (4): 613–635.
4. Shieber, Stuart (1985), "Evidence against the context-freeness of natural language" (PDF), Linguistics and Philosophy, 8 (3): 333–343, doi:10.1007/BF00630917.
5. John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman (2000). Introduction to Automata Theory, Languages, and Computation (2nd Edition). Pearson Education. ISBN 0-201-44124-1..
6. http://user.phil-fak.uni-duesseldorf.de/~kallmeyer/GrammarFormalisms/4nl-cfg.pdf
7. http://user.phil-fak.uni-duesseldorf.de/~kallmeyer/GrammarFormalisms/4lcfrs-intro.pdf
8. Laura Kallmeyer (2010). Parsing Beyond Context-Free Grammars. Springer Science & Business Media. pp. 1–5. ISBN 978-3-642-14846-0.