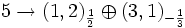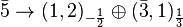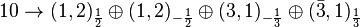Doublet–triplet splitting problem
In particle physics, the doublet–triplet (splitting) problem is a problem of some Grand Unified Theories, such as SU(5), SO(10), 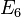 . Grand unified theories predict Higgs bosons (doublets of
. Grand unified theories predict Higgs bosons (doublets of 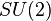 ) arise from representations of the unified group that contain other states, in particular, states that are triplets of color. The primary problem with these color triplet Higgs, is that they can mediate proton decay in supersymmetric theories that are only suppressed by two powers of GUT scale (i.e. they are dimension 5 supersymmetric operators). In addition to mediating proton decay, they alter gauge coupling unification. The doublet–triplet problem is the question 'what keeps the doublets light while the triplets are heavy?'
) arise from representations of the unified group that contain other states, in particular, states that are triplets of color. The primary problem with these color triplet Higgs, is that they can mediate proton decay in supersymmetric theories that are only suppressed by two powers of GUT scale (i.e. they are dimension 5 supersymmetric operators). In addition to mediating proton decay, they alter gauge coupling unification. The doublet–triplet problem is the question 'what keeps the doublets light while the triplets are heavy?'
Doublet–triplet splitting and the 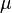 -problem
-problem
In 'minimal' SU(5), the way one accomplishes doublet–triplet splitting is through a combination of interactions
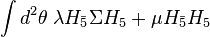
where  is an adjoint of SU(5) and is traceless. When
is an adjoint of SU(5) and is traceless. When 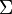 acquires a vacuum expectation value
acquires a vacuum expectation value
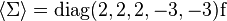
that breaks SU(5) to the Standard Model gauge symmetry the Higgs doublets and triplets acquire a mass
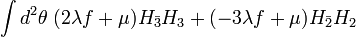
Since 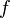 is at the GUT scale (
is at the GUT scale (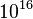 GeV) and the Higgs doublets need to have a weak scale mass (100 GeV), this requires
GeV) and the Higgs doublets need to have a weak scale mass (100 GeV), this requires
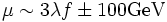 .
.
So to solve this doublet–triplet splitting problem requires a tuning of the two terms to within one part in 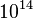 .
This is also why the mu problem of the MSSM (i.e. why are the Higgs doublets so light) and doublet–triplet splitting are so closely intertwined.
.
This is also why the mu problem of the MSSM (i.e. why are the Higgs doublets so light) and doublet–triplet splitting are so closely intertwined.
Dimopoulos–Wilczek mechanism
In an SO(10) theory, there is a potential solution to the doublet–triplet splitting problem known as the 'Dimopoulos–Wilczek' mechanism. In SO(10), the adjoint field, 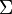 acquires a vacuum expectation value of the form
acquires a vacuum expectation value of the form
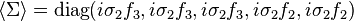 .
.
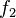 and
and 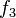 give masses to the Higgs doublet and triplet, respectively, and are independent of each other, because
give masses to the Higgs doublet and triplet, respectively, and are independent of each other, because 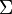 is traceless for any values they may have. If
is traceless for any values they may have. If 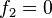 , then the Higgs doublet remains massless. This is very similar to the way that doublet–triplet splitting is done in either higher-dimensional grand unified theories or string theory.
, then the Higgs doublet remains massless. This is very similar to the way that doublet–triplet splitting is done in either higher-dimensional grand unified theories or string theory.
To arrange for the VEV to align along this direction (and still not mess up the other details of the model) often requires very contrived models, however.
Higgs representations in Grand Unified Theories
In SU(5):
In SO(10):
Proton decay
Non-supersymmetric theories suffer from quartic radiative corrections to the mass squared of the electroweak Higgs boson (see hierarchy problem). In the presence of supersymmetry, the triplet Higgsino needs to be more massive than the GUT scale to prevent proton decay because it generates dimension 5 operators in MSSM; there it is not enough simply to require the triplet to have a GUT scale mass.
References
- 'Supersymmetry at Ordinary Energies. 1. Masses AND Conservation Laws.' Steven Weinberg. Published in Phys.Rev.D26:287,1982.
- 'Proton Decay in Supersymmetric Models.' Savas Dimopoulos, Stuart A. Raby, Frank Wilczek. Published in Phys.Lett.B112:133,1982.
- 'Incomplete Multiplets in Supersymmetric Unified Models.' Savas Dimopoulos, Frank Wilczek.