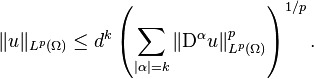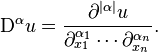Friedrichs' inequality

In mathematics, Friedrichs' inequality is a theorem of functional analysis, due to Kurt Friedrichs. It places a bound on the L^p norm of a function using L^p bounds on the weak derivatives of the function and the geometry of the domain, and can be used to show that certain norms on Sobolev spaces are equivalent. Friedrichs' inequality is a general case of the Poincaré–Wirtinger inequality which deals with the case $k=1$.

Statement of the inequality

Let 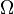$\Omega$ be a bounded subset of Euclidean space 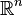$\mathbb R^n$ with diameter 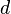$d$. Suppose that 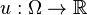$u:\Omega\to\mathbb R$ lies in the Sobolev space 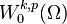$W_{0}^{k, p} (\Omega)$, i.e., 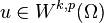$u\in W^{k,p}(\Omega)$ and the trace of 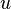$u$ on the boundary 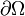$\partial\Omega$ is zero. Then

$\| u \|_{L^{p} (\Omega)} \leq d^{k} \left( \sum_{| \alpha | = k} \| \mathrm{D}^{\alpha} u \|_{L^{p} (\Omega)}^{p} \right)^{1/p}.$

In the above

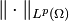• $\| \cdot \|_{L^{p} (\Omega)}$ denotes the L^p norm;
• α = (α₁, ..., α_n) is a multi-index with norm |α| = α₁ + ... + α_n;
• D^αu is the mixed partial derivative

$\mathrm{D}^{\alpha} u = \frac{\partial^{| \alpha |} u}{\partial_{x_{1}}^{\alpha_{1}} \cdots \partial_{x_{n}}^{\alpha_{n}} }.$

See also

• Poincaré inequality