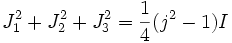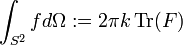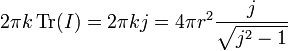Fuzzy sphere
In mathematics, the fuzzy sphere is one of the simplest and most canonical examples of non-commutative geometry. Ordinarily, the functions defined on a sphere form a commuting algebra. A fuzzy sphere differs from an ordinary sphere because the algebra of functions on it is not commutative. It is generated by spherical harmonics whose spin l is at most equal to some j. The terms in the product of two spherical harmonics that involve spherical harmonics with spin exceeding j are simply omitted in the product. This truncation replaces an infinite-dimensional commutative algebra by a 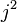 -dimensional non-commutative algebra.
-dimensional non-commutative algebra.
The simplest way to see this sphere is to realize this truncated algebra of functions as a matrix algebra on some finite-dimensional vector space.
Take the three j-dimensional matrices 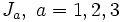 that form a basis for the j dimensional irreducible representation of the Lie algebra SU(2). They satisfy the relations
that form a basis for the j dimensional irreducible representation of the Lie algebra SU(2). They satisfy the relations ![[J_a,J_b]=i\epsilon_{abc}J_c](../I/m/50c73ac3fd64a4edd682965b3c76e366.png) , where
, where 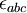 is the totally antisymmetric symbol with
is the totally antisymmetric symbol with 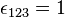 , and generate via the matrix product the algebra
, and generate via the matrix product the algebra  of j dimensional matrices. The value of the SU(2) Casimir operator in this representation is
of j dimensional matrices. The value of the SU(2) Casimir operator in this representation is
where I is the j-dimensional identity matrix.
Thus, if we define the 'coordinates'
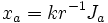 where r is the radius of the sphere and k is a parameter, related to r and j by
where r is the radius of the sphere and k is a parameter, related to r and j by 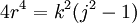 , then the above equation concerning the Casimir operator can be rewritten as
, then the above equation concerning the Casimir operator can be rewritten as
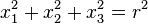 ,
,
which is the usual relation for the coordinates on a sphere of radius r embedded in three dimensional space.
One can define an integral on this space, by
where F is the matrix corresponding to the function f. For example, the integral of unity, which gives the surface of the sphere in the commutative case is here equal to
which converges to the value of the surface of the sphere if one takes j to infinity.
See also
- Fuzzy torus
Notes
- Jens Hoppe, "Membranes and Matrix Models", lectures presented during the summer school on ‘Quantum Field Theory – from a Hamiltonian Point of View’, August 2–9, 2000, arXiv:hep-th/0206192
- John Madore, An introduction to Noncommutative Differential Geometry and its Physical Applications, London Mathematical Society Lecture Note Series. 257, Cambridge University Press 2002
References
J. Hoppe, Quantum Theory of a Massless Relativistic Surface and a Two dimensional Bound State Problem. PhD thesis, Massachusetts Institute of Technology, 1982.