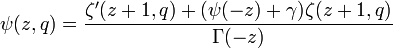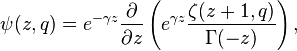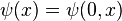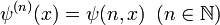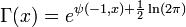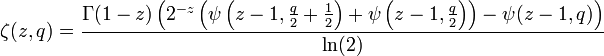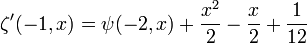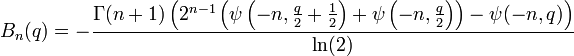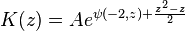Balanced polygamma function
In mathematics, the generalized polygamma function or balanced negapolygamma function is a function introduced by Olivier Espinosa Aldunate and Victor H. Moll.[1]
It generalizes the polygamma function to negative and fractional order, but remains equal to it for integer positive orders.
Definition
The generalized polygamma function is defined as follows:
or alternatively,
where 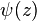 is the Polygamma function and
is the Polygamma function and 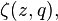 is the Hurwitz zeta function.
is the Hurwitz zeta function.
The function is balanced, in that it satisfies the conditions 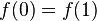 and
and 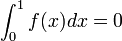 .
.
Relations
Several special functions can be expressed in terms of generalized polygamma function.
where 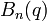 are Bernoulli polynomials
are Bernoulli polynomials
where K(z) is K-function and A is the Glaisher constant.
Special values
The balanced polygamma function can be expressed in a closed form at certain points:
-
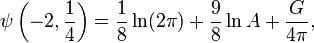 where
where  is the Glaisher constant and
is the Glaisher constant and 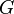 is the Catalan constant.
is the Catalan constant. -
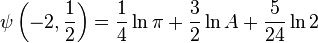
-
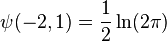
-
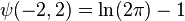
-
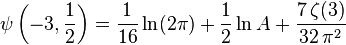
-
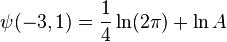
-
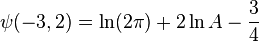
References
- ↑ Olivier Espinosa Victor H. Moll. A Generalized polygamma function. Integral Transforms and Special Functions Vol. 15, No. 2, April 2004, pp. 101–115