Hemi-cuboctahedron
| Hemi-cuboctahedron | |
|---|---|
 | |
| Type |
abstract polyhedron globally projective polyhedron |
| Faces |
7: 4 triangles 3 squares |
| Edges | 12 |
| Vertices | 6 |
| Vertex configuration | 3.4.3.4 |
| Schläfli symbol | r{3,4}/2 or r{3,4}3 |
| Symmetry group | S4, order 24 |
| Properties |
non-orientable Euler characteristic 1 |
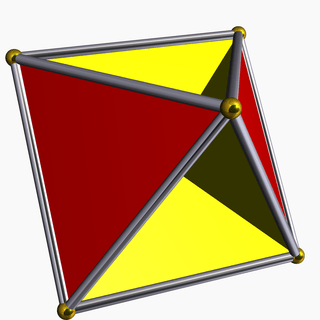
A hemi-cuboctahedron is an abstract polyhedron, containing half the faces of a semiregular cuboctahedron.
It has 4 triangular faces and 3 square faces, 12 edges, and 6 vertices. It can be seen as a rectified hemi-octahedron or rectified hemi-cube.
It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles and 3 square), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected.
Dual
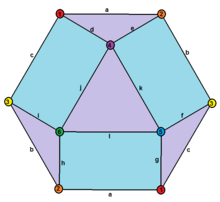
Its dual polyhedron is a rhombic hemi-dodecahedron which has 7 vertices (1-7), 12 edges (a-l), and 6 rhombic faces (A-F).
Related polyhedra
It has a real presentation as a uniform star polyhedron, the tetrahemihexahedron.
See also
References
- McMullen, Peter; Schulte, Egon (December 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0
External links
This article is issued from Wikipedia - version of the 10/22/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.