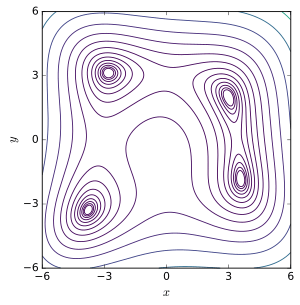
Himmelblau's function

Himmelblau's function

In 3D

Log-spaced down level curve plot ^[1]

In mathematical optimization, Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:

$f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}.\quad$

It has one local maximum at $x=-0.270845\,$ and $y=-0.923039\,$ where $f(x,y)=181.617\,$, and four identical local minima:

• $f(3.0,2.0)=0.0,\quad$
• $f(-2.805118,3.131312)=0.0,\quad$
• $f(-3.779310,-3.283186)=0.0,\quad$
• $f(3.584428,-1.848126)=0.0.\quad$

The locations of all the minima can be found analytically. However, because they are roots of cubic polynomials, when written in terms of radicals, the expressions are somewhat complicated.

The function is named after David Mautner Himmelblau (1924–2011), who introduced it.^[2]

See also

• Test functions for optimization

References

1. Simionescu, P.A. (2011). "Some Advancements to Visualizing Constrained Functions and Inequalities of Two Variables". Transactions of the ASME - Journal of Computing and Information Science in Engineering. 11 (1). doi:10.1115/1.3570770.
2. Himmelblau, D. (1972). Applied Nonlinear Programming. McGraw-Hill. ISBN 0-07-028921-2.