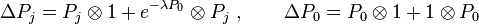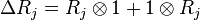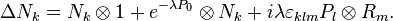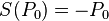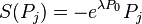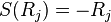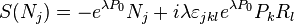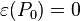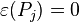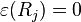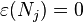K-Poincaré algebra
In physics and mathematics, the κ-Poincaré algebra, named after Henri Poincaré, is a deformation of the Poincaré algebra into an Hopf algebra. In the bicrossproduct basis, introduced by Majid-Ruegg[1] its commutation rules reads:
Where 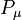 are the translation generators,
are the translation generators, 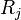 the rotations and
the rotations and 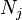 the boosts.
The coproducts are:
the boosts.
The coproducts are:
The antipodes and the counits:
The κ-Poincaré algebra is the dual Hopf algebra to the κ-Poincaré group, and can be interpreted as its “infinitesimal” version.
References
- ↑ Majid-Ruegg, Phys. Lett. B 334 (1994) 348, ArXiv:hep-th/9405107
This article is issued from Wikipedia - version of the 3/31/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![[P_\mu, P_\nu] = 0 \,](../I/m/0e2d29720bdc47cab5c43ac422c3e02c.png)
![[R_j , P_0] = 0, \; [R_j , P_k] = i \varepsilon_{jkl} P_l, \; [R_j , N_k] = i \varepsilon_{jkl} N_l, \; [R_j , R_k] = i \varepsilon_{jkl} R_l\,](../I/m/850926498fbf1325e147ec2163ff7991.png)
![[N_j , P_0] = i P_j, \;[N_j , P_k] = i \delta_{jk} \left( \frac{1 - e^{- 2 \lambda P_0}}{2 \lambda} + \frac{ \lambda }{2} |\vec{P}|^2 \right) - i \lambda P_j P_k, \; [N_j,N_k] = -i \varepsilon_{jkl} R_l\,](../I/m/69c4da5ebafec3e58bd2f73bfde9187a.png)