6174 (number)

← 6173 6174 6175 →
List of numbers — Integers ← 0 1k 2k 3k 4k 5k 6k 7k 8k 9k →
Cardinal	six thousand one hundred seventy-four
Ordinal	6174th (six thousand one hundred and seventy-fourth)
Factorization	2 × 3^2× 7^3
Roman numeral	VMCLXXIV
Binary	11000000111102
Ternary	221102003
Quaternary	12001324
Quinary	1441445
Senary	443306
Octal	140368
Duodecimal	36A612
Hexadecimal	181E16
Vigesimal	F8E20
Base 36	4RI36

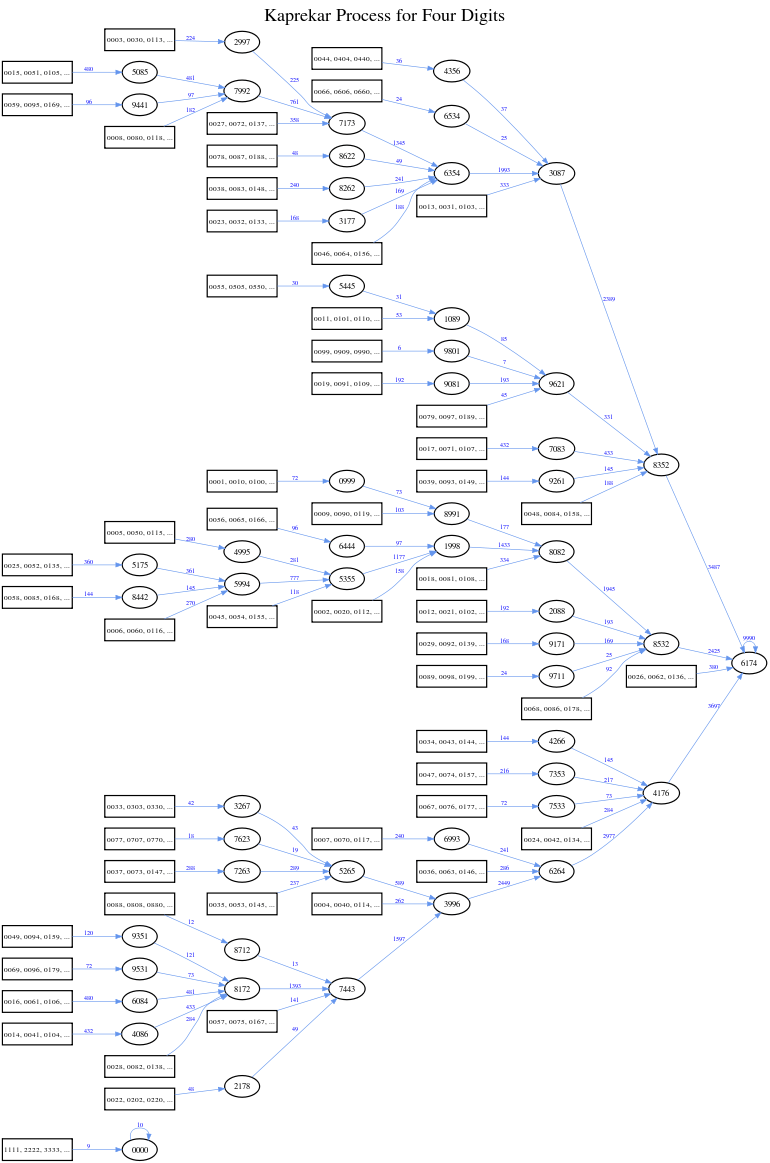
6174 is known as Kaprekar's constant^[1][2][3] after the Indian mathematician D. R. Kaprekar. This number is notable for the following property:

1. Take any four-digit number, using at least two different digits. (Leading zeros are allowed.)
2. Arrange the digits in descending and then in ascending order to get two four-digit numbers, adding leading zeros if necessary.
3. Subtract the smaller number from the bigger number.
4. Go back to step 2.

The above process, known as Kaprekar's routine, will always reach its fixed point, 6174, in at most 7 iterations.^[4] Once 6174 is reached, the process will continue yielding 7641 – 1467 = 6174. For example, choose 3524:

5432 – 2345 = 3087

8730 – 0378 = 8352

8532 – 2358 = 6174

7641 – 1467 = 6174

The only four-digit numbers for which Kaprekar's routine does not reach 6174 are repdigits such as 1111, which give the result 0000 after a single iteration. All other four-digit numbers eventually reach 6174 if leading zeros are used to keep the number of digits at 4:

2111 – 1112 = 0999

9990 – 0999 = 8991 (rather than 999 – 999 = 0)

9981 – 1899 = 8082

8820 – 0288 = 8532

8532 – 2358 = 6174

9831 reaches 6174 after 7 iterations:

9831 – 1389 = 8442

8442 – 2448 = 5994

9954 – 4599 = 5355

5553 – 3555 = 1998

9981 – 1899 = 8082

8820 – 0288 = 8532 (rather than 882 – 288 = 594)

8532 – 2358 = 6174

4371 reaches 6174 after 7 iterations:

7431 - 1347 = 6084

8640 - 0468 = 8172 (rather than 864 - 468 = 396)

8721 - 1278 = 7443

7443 - 3447 = 3996

9963 - 3699 = 6264

6642 - 2466 = 4176

7641 - 1467 = 6174

8774, 8477, 8747, 7748, 7487, 7847, 7784, 4877, 4787, and 4778 reach 6174 after 4 iterations:

8774 – 4778 = 3996

9963 – 3699 = 6264

6642 – 2466 = 4176

7641 – 1467 = 6174

Note that in each iteration of Kaprekar's routine, the two numbers being subtracted one from the other have the same digit sum and hence the same remainder modulo 9. Therefore, the result of each iteration of Kaprekar's routine is a multiple of 9.

Sequence of Kaprekar transformations ending in 6174

495 is the equivalent constant for three-digit numbers. For two-digit numbers, there is no equivalent constant; for any starting number with differing digits, the routine enters the loop (45, 9, 81, 63, 27, 45, … ). For each digit length greater than four, the routine may terminate at one of several fixed values or may enter one of several loops instead.^[4]

Sequence of three digit Kaprekar transformations ending in 495

Other numbers of digits

Digits of the given number	Cycles	Cycles length	Number of cycles
1	{0}	1	1
2	{00}, {09, 81, 63, 27, 45}	1, 5	2
3	{000}, {495}	1, 1	2
4	{0000}, {6174}	1, 1	2
5	{00000}, {53955, 59994}, {61974, 82962, 75933, 63954}, {62964, 71973, 83952, 74943}	1, 2, 4, 4	4
6	{000000}, {420876, 851742, 750843, 840852, 860832, 862632, 642654}, {549945}, {631764}	1, 7, 1, 1	4
7	{0000000}, {7509843, 9529641, 8719722, 8649432, 7519743, 8429652, 7619733, 8439552}	1, 8	2
8	{00000000}, {43208766, 85317642, 75308643, 84308652, 86308632, 86326632, 64326654}, {63317664}, {64308654, 83208762, 86526432}, {97508421}	1, 7, 1, 3, 1	5

See also

• Kaprekar number

References

1. Yutaka Nishiyama, Mysterious number 6174
2. Kaprekar DR (1955). "An Interesting Property of the Number 6174". Scripta Mathematica. 15: 244–245.
3. Kaprekar DR (1980). "On Kaprekar Numbers". Journal of Recreational Mathematics. 13 (2): 81–82.
4. Weisstein, Eric W. "Kaprekar Routine". MathWorld.

External links

• Bowley, Rover. "6174 is Kaprekar's Constant". Numberphile. University of Nottingham: Brady Haran.
• Sample (Perl) code to walk any four-digit number to Kaprekar's Constant