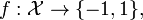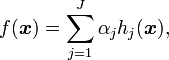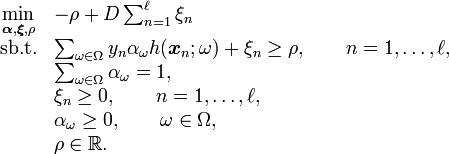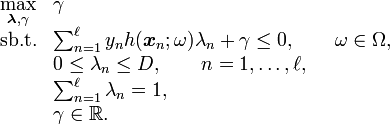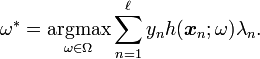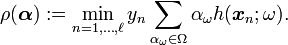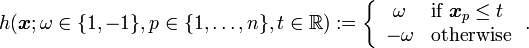LPBoost
Linear Programming Boosting (LPBoost) is a supervised classifier from the boosting family of classifiers. LPBoost maximizes a margin between training samples of different classes and hence also belongs to the class of margin-maximizing supervised classification algorithms. Consider a classification function
which classifies samples from a space 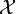 into one of two classes, labelled 1 and -1, respectively. LPBoost is an algorithm to learn such a classification function given a set of training examples with known class labels. LPBoost is a machine learning technique and especially suited for applications of joint classification and feature selection in structured domains.
into one of two classes, labelled 1 and -1, respectively. LPBoost is an algorithm to learn such a classification function given a set of training examples with known class labels. LPBoost is a machine learning technique and especially suited for applications of joint classification and feature selection in structured domains.
LPBoost overview
As in all boosting classifiers, the final classification function is of the form
where 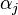 are non-negative weightings for weak classifiers
are non-negative weightings for weak classifiers 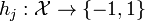 . Each individual weak classifier
. Each individual weak classifier 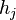 may be just a little bit better than random, but the resulting linear combination of many weak classifiers can perform very well.
may be just a little bit better than random, but the resulting linear combination of many weak classifiers can perform very well.
LPBoost constructs 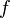 by starting with an empty set of weak classifiers. Iteratively, a single weak classifier to add to the set of considered weak classifiers is selected, added and all the weights
by starting with an empty set of weak classifiers. Iteratively, a single weak classifier to add to the set of considered weak classifiers is selected, added and all the weights 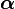 for the current set of weak classifiers are adjusted. This is repeated until no weak classifiers to add remain.
for the current set of weak classifiers are adjusted. This is repeated until no weak classifiers to add remain.
The property that all classifier weights are adjusted in each iteration is known as totally-corrective property. Early boosting methods, such as AdaBoost do not have this property and converge slower.
Linear program
More generally, let 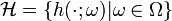 be the possibly infinite set of weak classifiers, also termed hypotheses. One way to write down the problem LPBoost solves is as a linear program with infinitely many variables.
be the possibly infinite set of weak classifiers, also termed hypotheses. One way to write down the problem LPBoost solves is as a linear program with infinitely many variables.
The primal linear program of LPBoost, optimizing over the non-negative weight vector 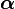 , the non-negative vector
, the non-negative vector  of slack variables and the margin
of slack variables and the margin 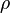 is the following.
is the following.
Note the effects of slack variables 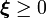 : their one-norm is penalized in the objective function by a constant factor
: their one-norm is penalized in the objective function by a constant factor 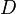 , which—if small enough—always leads to a primal feasible linear program.
, which—if small enough—always leads to a primal feasible linear program.
Here we adopted the notation of a parameter space 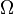 , such that for a choice
, such that for a choice 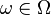 the weak classifier
the weak classifier 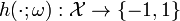 is uniquely defined.
is uniquely defined.
When the above linear program was first written down in early publications about boosting methods it was disregarded as intractable due to the large number of variables 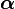 . Only later it was discovered that such linear programs can indeed be solved efficiently using the classic technique of column generation.
. Only later it was discovered that such linear programs can indeed be solved efficiently using the classic technique of column generation.
Column Generation for LPBoost
In a linear program a column corresponds to a primal variable. Column generation is a technique to solve large linear programs. It typically works in a restricted problem, dealing only with a subset of variables. By generating primal variables iteratively and on-demand, eventually the original unrestricted problem with all variables is recovered. By cleverly choosing the columns to generate the problem can be solved such that while still guaranteeing the obtained solution to be optimal for the original full problem, only a small fraction of columns has to be created.
LPBoost dual problem
Columns in the primal linear program corresponds to rows in the dual linear program. The equivalent dual linear program of LPBoost is the following linear program.
For linear programs the optimal value of the primal and dual problem are equal. For the above primal and dual problems, the optimal value is equal to the negative 'soft margin'. The soft margin is the size of the margin separating positive from negative training instances minus positive slack variables that carry penalties for margin-violating samples. Thus, the soft margin may be positive although not all samples are linearly separated by the classification function. The latter is called the 'hard margin' or 'realized margin'.
Convergence criterion
Consider a subset of the satisfied constraints in the dual problem. For any finite subset we can solve the linear program and thus satisfy all constraints. If we could prove that of all the constraints which we did not add to the dual problem no single constraint is violated, we would have proven that solving our restricted problem is equivalent to solving the original problem. More formally, let 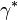 be the optimal objective function value for any restricted instance. Then, we can formulate a search problem for the 'most violated constraint' in the original problem space, namely finding
be the optimal objective function value for any restricted instance. Then, we can formulate a search problem for the 'most violated constraint' in the original problem space, namely finding 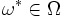 as
as
That is, we search the space 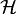 for a single decision stump
for a single decision stump 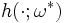 maximizing the left hand side of the dual constraint. If the constraint cannot be violated by any choice of decision stump, none of the corresponding constraint can be active in the original problem and the restricted problem is equivalent.
maximizing the left hand side of the dual constraint. If the constraint cannot be violated by any choice of decision stump, none of the corresponding constraint can be active in the original problem and the restricted problem is equivalent.
Penalization constant 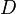
The positive value of penalization constant 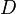 has to be found using model selection techniques. However, if we choose
has to be found using model selection techniques. However, if we choose 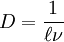 , where
, where  is the number of training samples and
is the number of training samples and 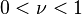 , then the new parameter
, then the new parameter 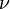 has the following properties.
has the following properties.
-
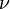 is an upper bound on the fraction of training errors; that is, if
is an upper bound on the fraction of training errors; that is, if 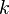 denotes the number of misclassified training samples, then
denotes the number of misclassified training samples, then 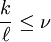 .
. -
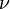 is a lower bound on the fraction of training samples outside or on the margin.
is a lower bound on the fraction of training samples outside or on the margin.
Algorithm
- Input:
- Training set
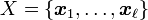 ,
, 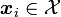
- Training labels
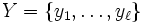 ,
, 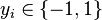
- Convergence threshold

- Training set
- Output:
- Classification function
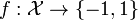
- Classification function
- Initialization
- Weights, uniform
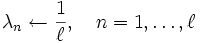
- Edge
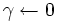
- Hypothesis count
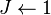
- Weights, uniform
- Iterate
-
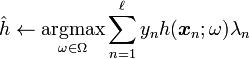
- if
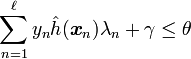 then
then
- break
-
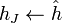
-
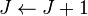
-
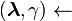 solution of the LPBoost dual
solution of the LPBoost dual -
 Lagrangian multipliers of solution to LPBoost dual problem
Lagrangian multipliers of solution to LPBoost dual problem
-
-
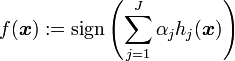
Note that if the convergence threshold is set to 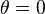 the solution obtained is the global optimal solution of the above linear program. In practice,
the solution obtained is the global optimal solution of the above linear program. In practice, 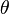 is set to a small positive value in order obtain a good solution quickly.
is set to a small positive value in order obtain a good solution quickly.
Realized margin
The actual margin separating the training samples is termed the realized margin and is defined as
The realized margin can and will usually be negative in the first iterations. For a hypothesis space that permits singling out of any single sample, as is commonly the case, the realized margin will eventually converge to some positive value.
Convergence guarantee
While the above algorithm is proven to converge, in contrast to other boosting formulations, such as AdaBoost and TotalBoost, there are no known convergence bounds for LPBoost. In practise however, LPBoost is known to converge quickly, often faster than other formulations.
Base learners
LPBoost is an ensemble learning method and thus does not dictate the choice of base learners, the space of hypotheses 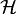 . Demiriz et al. showed that under mild assumptions, any base learner can be used. If the base learners are particularly simple, they are often referred to as decision stumps.
. Demiriz et al. showed that under mild assumptions, any base learner can be used. If the base learners are particularly simple, they are often referred to as decision stumps.
The number of base learners commonly used with Boosting in the literature is large. For example, if 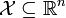 , a base learner could be a linear soft margin support vector machine. Or even more simple, a simple stump of the form
, a base learner could be a linear soft margin support vector machine. Or even more simple, a simple stump of the form
The above decision stumps looks only along a single dimension 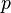 of the input space and simply thresholds the respective column of the sample using a constant threshold
of the input space and simply thresholds the respective column of the sample using a constant threshold 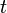 . Then, it can decide in either direction, depending on
. Then, it can decide in either direction, depending on 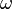 for a positive or negative class.
for a positive or negative class.
Given weights for the training samples, constructing the optimal decision stump of the above form simply involves searching along all sample columns and determining 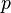 ,
, 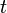 and
and 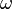 in order to optimize the gain function.
in order to optimize the gain function.
References
- Linear Programming Boosting via Column Generation, A. Demiriz and K.P. Bennett and J. Shawe-Taylor. Published 2002 in Kluwer Machine Learning 46, pages 225–254.