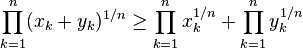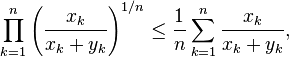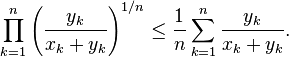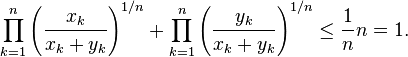Mahler's inequality

In mathematics, Mahler's inequality, named after Kurt Mahler, states that the geometric mean of the term-by-term sum of two finite sequences of positive numbers is greater than or equal to the sum of their two separate geometric means:

$\prod_{k=1}^n (x_k + y_k)^{1/n} \ge \prod_{k=1}^n x_k^{1/n} + \prod_{k=1}^n y_k^{1/n}$

when x_k, y_k > 0 for all k.

Proof

By the inequality of arithmetic and geometric means, we have:

$\prod_{k=1}^n \left({x_k \over x_k + y_k}\right)^{1/n} \le {1 \over n} \sum_{k=1}^n {x_k \over x_k + y_k},$

and

$\prod_{k=1}^n \left({y_k \over x_k + y_k}\right)^{1/n} \le {1 \over n} \sum_{k=1}^n {y_k \over x_k + y_k}.$

Hence,

$\prod_{k=1}^n \left({x_k \over x_k + y_k}\right)^{1/n} + \prod_{k=1}^n \left({y_k \over x_k + y_k}\right)^{1/n} \le {1 \over n} n = 1.$

Clearing denominators then gives the desired result.

See also

• Minkowski's inequality

References

• http://eom.springer.de/M/m064060.htm