Macroeconomic model

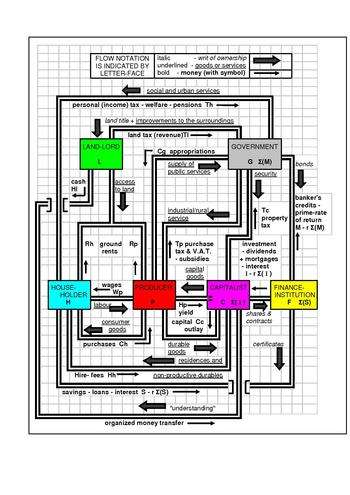
A macroeconomic model is an analytical tool designed to describe the operation of the economy of a country or a region. These models are usually designed to examine the dynamics of aggregate quantities such as the total amount of goods and services produced, total income earned, the level of employment of productive resources, and the level of prices.

Macroeconomic models may be logical, mathematical, and/or computational; the different types of macroeconomic models serve different purposes and have different advantages and disadvantages. Macroeconomics models may be used to clarify and illustrate basic theoretical principles; they may be used to test, compare, and quantify different macroeconomic theories; they may be used to produce "what if" scenarios (usually to predict the effects of changes in monetary, fiscal, or other macroeconomic policies); and they may be used to generate economic forecasts. Thus, macroeconomic models are widely used in academia, teaching and research, and are also widely used by international organizations, national governments and larger corporations, as well as by economics consultants and think tanks.

Types

Simple theoretical models

Simple text book descriptions of the macroeconomy involving a small number of equations or diagrams are often called ‘models’. Examples include the IS-LM model and Mundell–Fleming model of Keynesian macroeconomics, and the Solow model of neoclassical growth theory. These models share several features. They are based on a few equations involving a few variables, which can often be explained with simple diagrams.[1] Many of these models are static, but some are dynamic, describing the economy over many time periods. The variables that appear in these models often represent macroeconomic aggregates (such as GDP or total employment) rather than individual choice variables, and while the equations relating these variables are intended to describe economic decisions, they are not usually derived directly by aggregating models of individual choices. They are simple enough to be used as illustrations of theoretical points in introductory explanations of macroeconomic ideas; but therefore quantitative application to forecasting, testing, or policy evaluation is usually impossible without substantially augmenting the structure of the model.

Empirical forecasting models

In the 1940s and 1950s, as governments began accumulating national income and product accounting data, economists set out to construct quantitative models to describe the dynamics observed in the data.[2] These models estimated the relations between different macroeconomic variables using (mostly linear) time series analysis. Like the simpler theoretical models, these empirical models described relations between aggregate quantities, but many addressed a much finer level of detail (for example, studying the relations between output, employment, investment, and other variables in many different industries). Thus, these models grew to include hundreds or thousands of equations describing the evolution of hundreds or thousands of prices and quantities over time, making computers essential for their solution. While the choice of which variables to include in each equation was partly guided by economic theory (for example, including past income as a determinant of consumption, as suggested by the theory of adaptive expectations), variable inclusion was mostly determined on purely empirical grounds.[3]

Dutch economist Jan Tinbergen developed the first comprehensive national model, which he built for the Netherlands in 1936. He later applied the same modeling structure to the economies of the United States and the United Kingdom.[2] The first global macroeconomic model, Wharton Econometric Forecasting Associates' LINK project, was initiated by Lawrence Klein. The model was cited in 1980 when Klein, like Tinbergen before him, won the Nobel Prize. Large-scale empirical models of this type, including the Wharton model, are still in use today, especially for forecasting purposes.[4][5][6]

The Lucas critique of empirical forecasting models

Main article: Lucas critique

Econometric studies in the first part of the 20th century showed a negative correlation between inflation and unemployment called the Phillips curve.[7] Empirical macroeconomic forecasting models, being based on roughly the same data, had similar implications: they suggested that unemployment could be permanently lowered by permanently increasing inflation. However, in 1968, Milton Friedman[8] and Edmund Phelps[9] argued that this apparent tradeoff was illusory. They claimed that the historical relation between inflation and unemployment was due to the fact that past inflationary episodes had been largely unexpected. They argued that if monetary authorities permanently raised the inflation rate, workers and firms would eventually come to understand this, at which point the economy would return to its previous, higher level of unemployment, but now with higher inflation too. The stagflation of the 1970s appeared to bear out their prediction.[10]

In 1976, Robert Lucas, Jr., published an influential paper arguing that the failure of the Phillips curve in the 1970s was just one example of a general problem with empirical forecasting models.[11][12] He pointed out that such models are derived from observed relationships between various macroeconomic quantities over time, and that these relations differ depending on what macroeconomic policy regime is in place. In the context of the Phillips curve, this means that the relation between inflation and unemployment observed in an economy where inflation has usually been low in the past would differ from the relation observed in an economy where inflation has been high.[13] Furthermore, this means one cannot predict the effects of a new policy regime using an empirical forecasting model based on data from previous periods when that policy regime was not in place. Lucas argued that economists would remain unable to predict the effects of new policies unless they built models based on economic fundamentals (like preferences, technology, and budget constraints) that should be unaffected by policy changes.

Dynamic stochastic general equilibrium models

Partly as a response to the Lucas critique, economists of the 1980s and 1990s began to construct microfounded[14] macroeconomic models based on rational choice, which have come to be called dynamic stochastic general equilibrium (DSGE) models. These models begin by specifying the set of agents active in the economy, such as households, firms, and governments in one or more countries, as well as the preferences, technology, and budget constraint of each one. Each agent is assumed to make an optimal choice, taking into account prices and the strategies of other agents, both in the current period and in the future. Summing up the decisions of the different types of agents, it is possible to find the prices that equate supply with demand in every market. Thus these models embody a type of equilibrium self-consistency: agents choose optimally given the prices, while prices must be consistent with agents’ supplies and demands.

DSGE models often assume that all agents of a given type are identical (i.e. there is a ‘representative household’ and a ‘representative firm’) and can perform perfect calculations that forecast the future correctly on average (which is called rational expectations). However, these are only simplifying assumptions, and are not essential for the DSGE methodology; many DSGE studies aim for greater realism by considering heterogeneous agents[15] or various types of adaptive expectations.[16] Compared with empirical forecasting models, DSGE models typically have fewer variables and equations, mainly because DSGE models are harder to solve, even with the help of computers.[17] Simple theoretical DSGE models, involving only a few variables, have been used to analyze the forces that drive business cycles; this empirical work has given rise to two main competing frameworks called the real business cycle model[18][19][20] and the New Keynesian DSGE model.[21][22] More elaborate DSGE models are used to predict the effects of changes in economic policy and evaluate their impact on social welfare. However, economic forecasting is still largely based on more traditional empirical models, which are still widely believed to achieve greater accuracy in predicting the impact of economic disturbances over time.

DSGE versus CGE models

A closely related methodology that pre-dates DSGE modeling is computable general equilibrium (CGE) modeling. Like DSGE models, CGE models are often microfounded on assumptions about preferences, technology, and budget constraints. However, CGE models focus mostly on long-run relationships, making them most suited to studying the long-run impact of permanent policies like the tax system or the openness of the economy to international trade.[23][24] DSGE models instead emphasize the dynamics of the economy over time (often at a quarterly frequency), making them suited for studying business cycles and the cyclical effects of monetary and fiscal policy.

Agent-based computational macroeconomic models

Another modeling methodology which has developed at the same time as DSGE models is Agent-based computational economics (ACE), which is a variety of Agent-based modeling.[25] Like the DSGE methodology, ACE seeks to break down aggregate macroeconomic relationships into microeconomic decisions of individual agents. ACE models also begin by defining the set of agents that make up the economy, and specify the types of interactions individual agents can have with each other or with the market as a whole. Instead of defining the preferences of those agents, ACE models often jump directly to specifying their strategies. Or sometimes, preferences are specified, together with an initial strategy and a learning rule whereby the strategy is adjusted according to its past success.[26] Given these strategies, the interaction of large numbers of individual agents (who may be very heterogeneous) can be simulated on a computer, and then the aggregate, macroeconomic relationships that arise from those individual actions can be studied.

Strengths and weaknesses of DSGE and ACE models

DSGE and ACE models have different advantages and disadvantages due to their different underlying structures. DSGE models may exaggerate individual rationality and foresight, and understate the importance of heterogeneity, since the rational expectations, representative agent case remains the simplest and thus the most common type of DSGE model to solve. Also, unlike ACE models, it may be difficult to study local interactions between individual agents in DSGE models, which instead focus mostly on the way agents interact through aggregate prices. On the other hand, ACE models may exaggerate errors in individual decision-making, since the strategies assumed in ACE models may be very far from optimal choices unless the modeler is very careful. A related issue is that ACE models which start from strategies instead of preferences may remain vulnerable to the Lucas critique: a changed policy regime should generally give rise to changed strategies.

See also

References

  1. ↑ Blanchard, Olivier (2000), Macroeconomics, 2nd ed., Chap. 3.3, p. 47. Prentice Hall, ISBN 0-13-013306-X.
  2. 1 2 Klein, Lawrence (2004). "The contribution of Jan Tinbergen to economic science". De Economist. 152 (2): 155–157. doi:10.1023/B:ECOT.0000023251.14849.4f.
  3. ↑ Koopmans, Tjalling C. (1947). "Measurement Without Theory". Review of Economics and Statistics. 29 (3): 161–172. JSTOR 1928627.
  4. ↑ Klein, Lawrence R., ed. (1991). Comparative Performance of US Econometric Models. Oxford University Press. ISBN 0-19-505772-4.
  5. ↑ Eckstein, Otto (1983). The DRI Model of the US Economy. McGraw-Hill. ISBN 0-07-018972-2.
  6. ↑ Bodkin, Ronald; Klein, Lawrence; Marwah, Kanta (1991). A History of Macroeconometric Model Building. Edward Elgar.
  7. ↑ Phillips, A. W. (1958), "The relationship between unemployment and the rate of change of money wages in the United Kingdom 1861-1957", Economica, 25 (100): 283–299, doi:10.2307/2550759
  8. ↑ Friedman, Milton (1968), "The role of monetary policy", American Economic Review, American Economic Association, 58 (1): 1–17, JSTOR 1831652
  9. ↑ Phelps, Edmund S. (1968), "Money wage dynamics and labor market equilibrium", Journal of Political Economy, 76 (4): 678–711, doi:10.1086/259438
  10. ↑ Blanchard, Olivier (2000), op. cit., Ch. 28, p. 540.
  11. ↑ Lucas, Robert E., Jr. (1976), "Econometric Policy Evaluation: A Critique", Carnegie-Rochester Conference Series on Public Policy, 1: 19–46, doi:10.1016/S0167-2231(76)80003-6
  12. ↑ Hoover, Kevin D. (1988). "Econometrics and the Analysis of Policy". The New Classical Macroeconomics. Oxford: Basil Blackwell. pp. 167–209. ISBN 0-631-14605-9.
  13. ↑ Blanchard, Olivier (2000), op. cit., Ch. 28, p. 542.
  14. ↑ Edmund S. Phelps, ed., (1970), Microeconomic Foundations of Employment and Inflation Theory. New York, Norton and Co. ISBN 0-393-09326-3.
  15. ↑ Krusell, Per; Smith, Anthony A., Jr. (1998). "Income and wealth heterogeneity in the macroeconomy". Journal of Political Economy. 106 (5): 243–277. doi:10.1086/250034.
  16. ↑ George W. Evans and Seppo Honkapohja (2001), Learning and Expectations in Macroeconomics. Princeton University Press, ISBN 0-691-04921-1.
  17. ↑ DeJong, D. N. with C. Dave (2007), Structural Macroeconometrics. Princeton University Press, ISBN 0-691-12648-8.
  18. ↑ Kydland, Finn E.; Prescott, Edward C. (1982). "Time to Build and Aggregate Fluctuations". Econometrica. 50: 1345–70. doi:10.2307/1913386.
  19. ↑ Thomas F. Cooley (1995), Frontiers of Business Cycle Research. Princeton University Press.
  20. ↑ Andrew Abel and Ben Bernanke (1995), Macroeconomics, 2nd ed., Ch. 11.1, pp. 355-362. Addison-Wesley, ISBN 0-201-54392-3.
  21. ↑ Rotemberg, Julio J.; Woodford, Michael (1997). "An optimization-based econometric framework for the evaluation of monetary policy". NBER Macroeconomics Annual. 12: 297–346. JSTOR 3585236.
  22. ↑ Woodford, Michael (2003). Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press. ISBN 0-691-01049-8.
  23. ↑ Shoven, John B.; Whalley, John (1972). "A general equilibrium calculation of the effects of differential taxation of income from capital in the US". Journal of Public Economics. 1 (3–4): 281–321. doi:10.1016/0047-2727(72)90009-6.
  24. ↑ Kehoe, Patrick J.; Kehoe, Timothy J. (1994). "A primer on static applied general equilibrium models" (PDF). Federal Reserve Bank of Minneapolis Quarterly Review. 18 (1): 2–16.
  25. ↑ Tesfatsion, Leigh (2003). "Agent-Based Computational Economics" (PDF). Iowa State University Economics Working Paper #1.
  26. ↑ Brock, William; Hommes, Cars (1997). "A rational route to randomness". Econometrica. 65 (5): 1059–1095. JSTOR 2171879.

External links

This article is issued from Wikipedia - version of the 11/19/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.