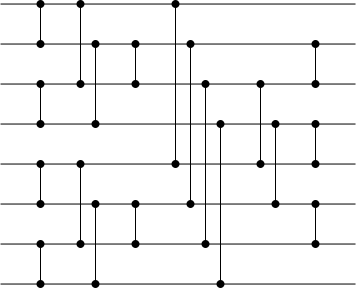
Batcher odd–even mergesort

Batcher odd–even mergesort

Visualization of the odd–even mergesort network with eight inputs
Class	Sorting algorithm
Data structure	Array
Worst-case performance	$O(\log ^{2}(n))$ parallel time
Best-case performance	$O(\log ^{2}(n))$ parallel time
Average performance	$O(\log ^{2}(n))$ parallel time
Worst-case space complexity	$O(n\log ^{2}(n))$ non-parallel time

Batcher's odd–even mergesort is a generic construction devised by Ken Batcher for sorting networks of size O(n (log n)²) and depth O((log n)²), where n is the number of items to be sorted. Although it is not asymptotically optimal, Knuth concluded in 1998, with respect to the AKS network that "Batcher's method is much better, unless n exceeds the total memory capacity of all computers on earth!"^[1]

It is popularized by the second GPU Gems book,^[2] as an easy way of doing reasonably efficient sorts on graphics-processing hardware.

Example code

The following is an implementation of odd–even mergesort algorithm in Python. The input is a list x of length a power of 2. The output is a list sorted in ascending order.

def oddeven_merge(lo, hi, r):
    step = r * 2
    if step < hi - lo:
        yield from oddeven_merge(lo, hi, step)
        yield from oddeven_merge(lo + r, hi, step)
        yield from [(i, i + r) for i in range(lo + r, hi - r, step)]
    else:
        yield (lo, lo + r)

def oddeven_merge_sort_range(lo, hi):
    """ sort the part of x with indices between lo and hi.

    Note: endpoints (lo and hi) are included.
    """
    if (hi - lo) >= 1:
        # if there is more than one element, split the input
        # down the middle and first sort the first and second
        # half, followed by merging them.
        mid = lo + ((hi - lo) // 2)
        yield from oddeven_merge_sort_range(lo, mid)
        yield from oddeven_merge_sort_range(mid + 1, hi)
        yield from oddeven_merge(lo, hi, 1)

def oddeven_merge_sort(length):
    """ "length" is the length of the list to be sorted.
    Returns a list of pairs of indices starting with 0 """
    yield from oddeven_merge_sort_range(0, length - 1)

def compare_and_swap(x, a, b):
    if x[a] > x[b]:
        x[a], x[b] = x[b], x[a]

>>> data = [2, 4, 3, 5, 6, 1, 7, 8]
>>> pairs_to_compare = list(oddeven_merge_sort(len(data)))
>>> pairs_to_compare
[(0, 1), (2, 3), (0, 2), (1, 3), (1, 2), (4, 5), (6, 7), (4, 6), (5, 7), (5, 6), (0, 4), (2, 6), (2, 4), (1, 5), (3, 7), (3, 5), (1, 2), (3, 4), (5, 6)]
>>> for i in pairs_to_compare: compare_and_swap(data, *i)
>>> data
[1, 2, 3, 4, 5, 6, 7, 8]

More concise and non-recursive calculation of partner node is possible. Here is a Scala implementation to get the partner of an index at each step:^[3]

  def partner(index: Int, merge: Int, step: Int): Int = {
    if (step == 1)
      index ^ (1 << (merge - 1))
    else {
      val (scale, box) = (1 << (merge - step), 1 << step)
      val sn = index / scale - (index / scale / box) * box

      if (sn == 0 || sn == box - 1) index // no exchange at this level
      else if (sn % 2 == 0) index - scale else index + scale
    }
  }

See also

• Bitonic sorter

References

1. D.E. Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1998. ISBN 0-201-89685-0. Section 5.3.4: Networks for Sorting, pp. 219–247.
2. http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter46.html
3. "Sorting network from Batcher's Odd-Even merge: partner calculation". Renat Bekbolatov. Retrieved 7 May 2015.

External links

• Odd–even mergesort at fh-flensburg.de
• Odd-even mergesort network generator Interactive Batcher's Odd-Even merge-based sorting network generator.