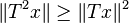Paranormal operator

In mathematics, especially operator theory, a paranormal operator is a generalization of a normal operator. More precisely, a bounded linear operator T on a complex Hilbert space H is said to be paranormal if:

$\|T^2x\| \ge \|Tx\|^2 \,$

for every unit vector x in H.

The class of paranormal operators was introduced by V. Istratescu in 1960s, though the term "paranormal" is probably due to Furuta.^[1][2]

Every hyponormal operator (in particular, a subnormal operator, a quasinormal operator and a normal operator) is paranormal. If T is a paranormal, then Tⁿ is paranormal.^[2] On the other hand, Halmos gave an example of a hyponormal operator T such that T² isn't hyponormal. Consequently, not every paranormal operator is hyponormal.^[3]

A compact paranormal operator is normal.^[4]

References

1. V. Istratescu. On some hyponormal operators
2. Furuta, Takayuki. On the Class of Paranormal Operators
3. P.R.Halmos, A Hilbert Space Problem Book 2nd edition, Springer-Verlag, New York, 1982.
4. Furuta, Takayuki. Certain Convexoid Operators