Parity anomaly

In theoretical physics a quantum field theory is said to have a parity anomaly if its classical action is invariant under a change of parity of the universe, but the quantum theory is not invariant.

This kind of anomaly can occur in odd-dimensional gauge theories with fermions whose gauge groups have odd dual Coxeter numbers. They were first introduced by Antti J. Niemi and Gordon Walter Semenoff in the letter Axial-Anomaly-Induced Fermion Fractionization and Effective Gauge-Theory Actions in Odd-Dimensional Space-Times and by A. Norman Redlich in the letter Gauge Noninvariance and Parity Nonconservation of Three-Dimensional Fermions and the article Parity violation and gauge noninvariance of the effective gauge field action in three dimensions. It is in some sense an odd-dimensional version of Edward Witten's SU(2) anomaly in 4-dimensions, and in fact Redlich writes that his demonstration follows Witten's.

The anomaly in 3-dimensions

Consider a classically parity-invariant gauge theory whose gauge group G has dual coxeter number h in 3-dimensions. Include n Majorana fermions which transform under a real representation of G. This theory naively suffers from an ultraviolet divergence. If one includes a gauge-invariant regulator then the quantum parity invariance of the theory will be broken if h and n are odd.

Sketch of the demonstration

The anomaly can only be a choice of sign

Consider for example Pauli–Villars regularization. One needs to add n massive Majorana fermions with opposite statistics and take their masses to infinity. The complication arises from the fact that the 3-dimensional Majorana mass term, 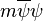$m\overline{\psi}\psi$ is not parity invariant, therefore the possibility exists that the parity invariance may remain when the mass goes to infinity. Indeed, this is the source of the anomaly.

If n is even, then one may rewrite the n Majorana fermions as n/2 Dirac fermions. These have parity invariant mass terms, and so Pauli–Villars may be used to regulate the divergences and no parity anomaly arises. Therefore for even n there is no anomaly. Moreover, as the contribution of 2n Majorana fermions to the partition function is the square of the contribution of n fermions, the square of the contribution to the anomaly of n fermions must be equal to one. Therefore the anomalous phase may only be equal to a square root of one, in other words, plus or minus one. If it is equal to one, then there is no anomaly. Therefore the question is, when is there an ambiguity in the partition function of a factor of -1.

Anomaly from the index theorem

We want to know when the choice of sign of the partition function is ill-defined. The possibility that it be ill-defined exists because the action contains the fermion kinetic term

$i\overline{\psi}(\partial_\mu+A_\mu)\Gamma^\mu\psi$

where Ψ is a Majorana fermion and A is the vector potential. In the path integral, the exponential of the action is integrated over all of the fields. When integrating the above term over the fermion fields one obtains a factor of the square root of the determinant of the Dirac operator for each of the n Majorana fermions.

As is usual with a square root, one needs to determine its sign. The overall phase of the partition function is not an observable in quantum mechanics, and so for a given configuration this sign choice can be made arbitrarily. But one needs to check that the sign choice is consistent. To do this, let us deform the configuration through the configuration space, on a path which eventually returns to the original configuration. If the sign choice was consistent then, having returned to the original configuration, one will have the original sign. This is what needs to be checked.

The original spacetime is 3-dimensional, call the space M. Now we are considering a circle in configuration space, which is the same thing as a single configuration on the space $M\times S^1$. To find out the number of times that the sign of the square root vanishes as one goes around the circle, it suffices to count the number of zeroes of the determinant on $M\times S^1$, because each time that a pair of eigenvalues changes sign there will be a zero. Notice that the eigenvalues come in pairs, as discussed for example in Supersymmetric Index Of Three-Dimensional Gauge Theory, and so whenever one eigenvalue crosses zero, two will cross.

Summarizing, we want to know how many times the sign of the square root of the determinant of a Dirac operator changes sign as one circumnavigates the circle. The eigenvalues of the Dirac operator come in pairs, and the sign changes each time a pair crosses zero. Thus we are counting the zeroes of the Dirac operator on the space $M\times S^1$. These zeroes are counted by the Atiyah-Singer index theorem, which gives the answer h times the second Chern class of the gauge bundle over $M\times S^1$. This second Chern class may be any integer. In particular it may be one, in which case the sign changes h times. If the sign changes an odd number of times then the partition function is ill-defined, and so there is an anomaly.

In conclusion, we have found that there is an anomaly if the number n of Majorana fermions is odd and if the dual Coxeter number h of the gauge group is also odd.

Chern–Simons gauge theories

3-dimensional Chern–Simons gauge theories are also anomalous when their level is half-integral. In fact, the derivation is identical to that above. Using Stokes' theorem and the fact that the exterior derivative of the Chern–Simons action is equal to the instanton number, the 4-dimensional theory on $M\times S^1$ has a theta angle equal to the level of the Chern–Simons theory, and so the 4-dimensional partition function is equal to -1 precisely when the instanton number is odd. This implies that the 3-dimensional partition function is ill-defined by a factor of -1 when considering deformations over a path with an odd number of instantons.

Fractional quantization conditions

In particular, the anomalies coming from fermions and the half-level Chern–Simons terms will cancel if and only if the number of Majorana fermions plus twice the Chern–Simons level is even. In the case n=1, this statement is the half-integer quantization condition in 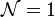$\mathcal{N}=1$ supersymmetric Chern–Simons gauge theories presented in The Chern-Simons Coefficient in Supersymmetric Yang-Mills Chern-Simons Theories. When n=2 this contribution to the partition function was found in 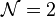$\mathcal{N}=2$ and 3 gauge theories in Branes and Supersymmetry Breaking in Three Dimensional Gauge Theories.

One-loop correction to the Chern–Simons level

The fact that both Chern–Simons terms and Majorana fermions are anomalous under deformations with odd instanton numbers is not a coincidence. When the Pauli–Villars mass for n Majorana fermions is taken to infinity, Redlich found that the remaining contribution to the partition function is equal to a Chern–Simons term at level −n/2. This means in particular that integrating out n charged Majorana fermions renormalizes the Chern–Simons level of the corresponding gauge theory by −n/2. The fact that the Chern–Simons level is only allowed to take discrete values implies that the coupling constant can not enter into the correction to the level. This only occurs for the 1-loop correction, therefore the contribution of the Majorana fermions to the Chern–Simons level may be precisely calculated at 1-loop and all higher loop corrections vanish.