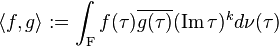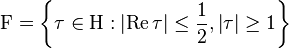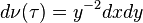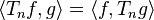Petersson inner product
In mathematics the Petersson inner product is an inner product defined on the space of entire modular forms. It was introduced by the German mathematician Hans Petersson.
Definition
Let 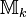 be the space of entire modular forms of weight
be the space of entire modular forms of weight 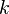 and
and
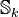 the space of cusp forms.
the space of cusp forms.
The mapping 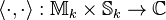 ,
,
is called Petersson inner product, where
is a fundamental region of the modular group 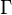 and for
and for 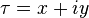
is the hyperbolic volume form.
Properties
The integral is absolutely convergent and the Petersson inner product is a positive definite Hermitian form.
For the Hecke operators 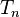 , and for forms
, and for forms 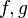 of level
of level 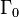 , we have:
, we have:
This can be used to show that the space of cusp forms of level 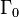 has an orthonormal basis consisting of
simultaneous eigenfunctions for the Hecke operators and the Fourier coefficients of these
forms are all real.
has an orthonormal basis consisting of
simultaneous eigenfunctions for the Hecke operators and the Fourier coefficients of these
forms are all real.
References
- T.M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Springer Verlag Berlin Heidelberg New York 1990, ISBN 3-540-97127-0
- M. Koecher, A. Krieg, Elliptische Funktionen und Modulformen, Springer Verlag Berlin Heidelberg New York 1998, ISBN 3-540-63744-3
- S. Lang, Introduction to Modular Forms, Springer Verlag Berlin Heidelberg New York 2001, ISBN 3-540-07833-9