Proportional control

The fly-ball governor is a classic example of proportional control.

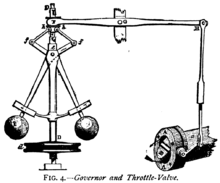
A proportional control system is a type of linear feedback control system. Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor.

The proportional control system is more complex than an on-off control system like a bi-metallic domestic thermostat, but simpler than a proportional-integral-derivative (PID) control system used in something like an automobile cruise control. On-off control will work where the overall system has a relatively long response time, but can result in instability if the system being controlled has a rapid response time. Proportional control overcomes this by modulating the output to the controlling device, such as a continuously variable valve.

An analogy to on-off control is driving a car by applying either full power or no power and varying the duty cycle, to control speed. The power would be on until the target speed is reached, and then the power would be removed, so the car reduces speed. When the speed falls below the target, with a certain hysteresis, full power would again be applied. It can be seen that this looks like pulse-width modulation, but would obviously result in poor control and large variations in speed. The more powerful the engine; the greater the instability, the heavier the car; the greater the stability. Stability may be expressed as correlating to the power-to-weight ratio of the vehicle.

Proportional control is how most drivers control the speed of a car. If the car is at target speed and the speed increases slightly, the power is reduced slightly, or in proportion to the error (the actual versus target speed), so that the car reduces speed gradually and reaches the target point with very little, if any, "overshoot", so the result is much smoother control than on-off control.

Further refinements like PID control would help compensate for additional variables like hills, where the amount of power needed for a given speed change would vary. This would be accounted for by the integral function of the PID control.

Proportional Control Theory

In the proportional control algorithm, the controller output is proportional to the error signal, which is the difference between the setpoint and the process variable. In other words, the output of a proportional controller is the multiplication product of the error signal and the proportional gain.

This can be mathematically expressed as

$P_{{{\mathrm {out}}}}=K_{p}\,{e(t)+p0}$

where

• $p0$: Controller output with zero error.
• $P_{{{\mathrm {out}}}}$: Output of the proportional controller
• $K_{p}$: Proportional gain
• $e(t)$: Instantaneous process error at time t. $e(t)=SP-PV$
• SP: Set point
• PV: Process variable

Constraints: $P_{{{\mathrm {out}}}}$ cannot be greater than 1 (fractional) or 100%. $P_{{{\mathrm {out}}}}$ can be less than 0 when the controller is in "cooling mode" rather than "heating mode". In any case $P_{{{\mathrm {out}}}}$ cannot be less than -1 or -100%. On a real plant valves cannot open more than 100% however mathematical models may summon from nowhere, greater outputs than physically possible absent these constraints.

Qualifications: It is preferable to express $K_{p}$ as a pure number. To do this $e(t)$ should be written as a ratio with the span of the instrument. This span is in the same units as error (e.g. C degrees) so the ratio is pure number.

Offset Error

Proportional Control Action leaves out an error called Offset Error. Once a disturbance (deviation from existing state) occurs in the Steady State Condition, any corrective control action, based purely on Proportional Control, will always leave out an error between the next steady state and the desired setpoint. This error is called an Offset Error.

Proportional Band

Proportional Band is the band of Controller Output over which the Final Control Element (a Control Valve, for instance) will move from one extreme to another. Mathematically, it can be expressed as:
$PB = \frac{100}{K_p}\$

So if $K_{p}$, the Proportional Gain, is very high, the Proportional Band is very small, which means that the Band of Controller Output, over which the final Control Element, like a Control Valve, will go from minimum to maximum (or vice versa) is very small. This is the case with ON-OFF Controllers, where $K_{p}$ is very high and hence, for even a small error, the Controller Output is driven from one extreme to another.

See also

• PI controller - special case of PID controller

External links

• Proportional control compared to ON-OFF or bang-bang control d vvg