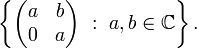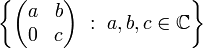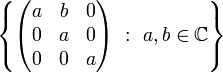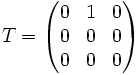Reflexive operator algebra
In functional analysis, a reflexive operator algebra A is an operator algebra that has enough invariant subspaces to characterize it. Formally, A is reflexive if it is equal to the algebra of bounded operators which leave invariant each subspace left invariant by every operator in A.
This should not be confused with a reflexive space.
Examples
Nest algebras are examples of reflexive operator algebras. In finite dimensions, these are simply algebras of all matrices of a given size whose nonzero entries lie in an upper-triangular pattern.
In fact if we fix any pattern of entries in an n by n matrix containing the diagonal, then the set of all n by n matrices whose nonzero entries lie in this pattern forms a reflexive algebra.
An example of an algebra which is not reflexive is the set of 2 by 2 matrices
This algebra is smaller than the Nest algebra
but has the same invariant subspaces, so it is not reflexive.
If T is a fixed n by n matrix then the set of all polynomials in T and the identity operator forms a unital operator algebra. A theorem of Deddens and Fillmore states that this algebra is reflexive if and only if the largest two blocks in the Jordan normal form of T differ in size by at most one. For example, the algebra
which is equal to the set of all polynomials in
and the identity is reflexive.
Hyper-reflexivity
Let 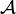 be a weak*-closed operator algebra contained in B(H), the set of all bounded operators on a Hilbert space H and for T any operator in B(H), let
be a weak*-closed operator algebra contained in B(H), the set of all bounded operators on a Hilbert space H and for T any operator in B(H), let
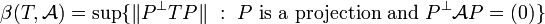 .
.
Observe that P is a projection involved in this supremum precisely if the range of P is an invariant subspace of 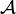 .
.
The algebra 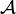 is reflexive if and only if for every T in B(H):
is reflexive if and only if for every T in B(H):
 .
.
We note that for any T in B(H) the following inequality is satisfied:
 .
.
Here 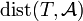 is the distance of T from the algebra, namely the smallest norm of an operator T-A where A runs over the algebra. We call
is the distance of T from the algebra, namely the smallest norm of an operator T-A where A runs over the algebra. We call 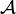 hyperreflexive if there is a constant K such that for every operator T in B(H),
hyperreflexive if there is a constant K such that for every operator T in B(H),
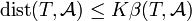 .
.
The smallest such K is called the distance constant for 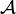 . A hyper-reflexive operator algebra is automatically reflexive.
. A hyper-reflexive operator algebra is automatically reflexive.
In the case of a reflexive algebra of matrices with nonzero entries specified by a given pattern, the problem of finding the distance constant can be rephrased as a matrix-filling problem: if we fill the entries in the complement of the pattern with arbitrary entries, what choice of entries in the pattern gives the smallest operator norm?
Examples
- Every finite-dimensional reflexive algebra is hyper-reflexive. However, there are examples of infinite-dimensional reflexive operator algebras which are not hyper-reflexive.
- The distance constant for a one-dimensional algebra is 1.
- Nest algebras are hyper-reflexive with distance constant 1.
- Many von Neumann algebras are hyper-reflexive, but it is not known if they all are.
- A type I von Neumann algebra is hyper-reflexive with distance constant at most 2.
See also
- Invariant subspace
- subspace lattice
- reflexive subspace lattice
- nest algebra
References
- William Arveson, Ten lectures on operator algebras, ISBN 0-8218-0705-6
- H. Radjavi and P. Rosenthal, Invariant Subspaces, ISBN 0-486-42822-2