Run-length limited
Run length limited or RLL coding is a line coding technique that is used to send arbitrary data over a communications channel with bandwidth limits. RLL codes are defined by four main parameters: m, n, d, k. The first two m/n refer to the rate of the code, while the remaining two specify the minimum d and maximum k number of zeroes between consecutive ones. This is used in both telecommunication and storage systems which move a medium past a fixed recording head.
Specifically, RLL bounds the length of stretches (runs) of repeated bits during which the signal does not change. If the runs are too long, clock recovery is difficult; if they are too short, the high frequencies might be attenuated by the communications channel. By modulating the data, RLL reduces the timing uncertainty in decoding the stored data, which would lead to the possible erroneous insertion or removal of bits when reading the data back. Run-length limited codes were widely used in hard disk drives until the mid-1980s, and are still used in digital optical discs such as CD, DVD, MD, Hi-MD and Blu-ray. This mechanism ensures that the boundaries between bits can always be accurately found (preventing bit slip), while efficiently using the media to reliably store the maximum amount of data in a given space.
Early disk drives used very simple encoding schemes, such as RLL (0,1) FM code, but higher density RLL (2,7) and RLL (1,7) codes became the de facto industry standard for hard disks by the early 1990s.
Need for RLL coding
On a hard disk drive, information is represented by changes in the direction of the magnetic field on the disk. In a computer, information is represented by the voltage on a wire. No voltage on the wire in relation to a defined ground level would be a binary zero, and a positive voltage on the wire in relation to ground represents a binary one. Magnetic media, on the other hand, always carries a magnetic flux - either a "north" pole or a "south" pole. In order to convert the magnetic fields to binary data, some encoding method must be used to translate between the two.
One of the simplest practical codes, Modified Non-Return-to-Zero-Inverted (NRZI), simply encodes a 1 as a magnetic polarity transition, also known as a "flux reversal", and a zero as no transition. With the disk spinning at a constant rate, each bit is given an equal time period, a "data window," for the magnetic signal that represents that bit, and the flux reversal, if any, occurs at the start of this window. (Note: older hard disks used one fixed length of time as the data window over the whole disk, but modern disks are more complicated; for more on this, see zoned bit recording.)
While this method is simple, it is prone to errors for long runs of zeros.
In a simple example, consider the binary pattern 101 with a data window of 1 ns (one nanosecond, or one billionth of a second). This will be stored on the disk as a change, followed by no change, and then another change. If the preceding magnetic polarity was already positive, the resulting pattern might look like this: −−+. A value of 255, or all binary ones, would be written as −+−+−+−+ or +−+−+−+−. A zero byte would be written as ++++++++ or −−−−−−−−. A 512 byte sector of zeros would be written as 4,096 sequential bits with the same polarity.
Since a disk drive is a physical piece of hardware, the rotational speed of the drive can change slightly, due to a change in the motor speed or thermal expansion of the disk platter. The physical media on a floppy disk can also become deformed, causing larger timing errors, and the timing circuit on the controller itself may have small variations in speed. The problem is that, with a long string of zeros, there's no way for the disk drive's controller to know the exact position of the read head, and thus no way to know exactly how many zeros there are. A speed variation of even 0.1% - which is more precise than any practical floppy drive - could result in four bits being added to or removed from the 4,096 bit data stream. Without some form of synchronization and error correction, the data would become completely unusable.
The other problem is due to the limits of magnetic media itself: it is only possible to write so many polarity changes in a certain amount of space, so there's an upper limit to how many 1's can also be written sequentially.
To prevent this problem, data is coded in such a way that long repetitions of a single binary value do not occur. By limiting the number of zeros written consecutively, this makes it possible for the drive controller to stay in sync. By limiting the number of 1's written in a row, the overall frequency of polarity changes is reduced, allowing the drive to store more data in the same amount of space, resulting in either a smaller package for the same amount of data or more storage in the same size package.
History
All codes used to record on magnetic disks have limited the run of zero transitions and can therefore be characterized as RLL codes. The earliest and simplest variants were given specific names, such as Modified Frequency Modulation (MFM); often, "RLL" refers only to the more complex variants not given such specific names, but that is technically incorrect.
The RLL terminology in hard disk drive art, specifically RLL (2,7), was originally developed by IBM engineers, and was first used commercially in 1979 on the IBM 3370 DASD,[1][2][3] for use with the 4300 series mainframe. During the late 1980s, PC hard disks began using RLL proper (i.e. variants more complex than those that had received their own proper names, such as MFM). RLL codes have found almost universal application in optical disc recording practice since 1980. In consumer electronics, RLLs like the EFM code (with Eight-to-Fourteen:rate = 8/14, d=2, k=10) are employed in the Compact Disc (CD) and MiniDisc (MD), and the EFMPlus code (rate = 8/16, d=2, k=10) used in the DVD. Parameters d, k are the minimum and maximum allowed run-lengths. For more coverage on the storage technologies, the references cited in this article are useful.[4][5]
Technical overview
Generally run-length is the number of bits for which signal remains unchanged. A run-length of 3 for bit 1, represents a sequence of '111'. For instance, the pattern of magnetic polarizations on the disk might be '+−−−−++−−−++++++', with runs of length 1, 4, 2, 3, and 6. However, run length limited coding terminology assumes NRZI encoding, so 1 bits indicate changes and 0 bits indicate the absence of change, the above sequence would be expressed as '11000101001000001', and only runs of zero bits are counted.
Somewhat confusingly, the run length is the number of zeros (0, 3, 1, 2 and 5 in the preceding) between adjacent ones, which is one less than the number of bit times the signal actually remains unchanged. Run length limited sequences are characterized by two parameters, d and k, which stipulate the minimum and maximum zero-bit run length that can occur in the sequence. So RLL codes are generally specified as (d,k) RLL. e.g.: (1,3) RLL.
Coding
In the encoded format a "1" bit indicates a flux transition, while a "0" indicates that the magnetic field on the disk does not change for that time interval.
FM: (0,1) RLL
Generally, the term "RLL code" is used to refer to more elaborate encodings, but the original frequency modulation code, also called differential Manchester, can be seen as a simple rate-1/2 RLL code. The added 1 bits are referred to as clock bits.
| Data | Encoded |
|---|---|
| 0 | 10 |
| 1 | 11 |
Example:
Data: 0 0 1 0 1 1 0 1 0 0 0 1 1 0 Encoded: 1010111011111011101010111110 Clock: 1 1 1 1 1 1 1 1 1 1 1 1 1 1
GCR: (0,2) RLL
By extending the maximum run length to 2 adjacent 0 bits, the data rate can be improved to 4/5. This is the original IBM group code recording variant.
|
|
Example:
Data: 0010 1101 0001 1000 Encoded: 10010011011101111010
Note that to meet the definition of (0,2) RLL, it is not sufficient only that each 5-bit code contain no more than two consecutive zeros, but it is also necessary that any pair of 5-bit codes as a combined sequentially not contain more than two consecutive zeros. That is, there must not be more than two zeros between the last one bit in the first code and the first one bit in the second code, for any two arbitrarily chosen codes. This is required because for any RLL code, the run length limits—0 and 2 in this case—apply to the overall modulated bitstream, not just to the components of it that represent discrete sequences of plain data bits. (This rule must hold for any arbitrary pair of codes, without exception, because the input data may be any arbitrary sequence of bits.) The IBM GCR code above meets this condition, since the maximum run length of zeros at the beginning of any 5-bit code is one, and likewise the maximum run length at the end of any code is one, making a total run length of two at the junction between adjacent codes. (An example of the maximum run length occurring between codes can be seen in the example given above, where the code for the data "0010" ends with a zero and the code for the next data, "1101", begins with a zero, forming a run of two zeros at the junction of these two 5-bit codes.)
MFM: (1,3) RLL
Modified frequency modulation begins to get interesting, because its special properties allow its bits to be written to a magnetic medium with twice the density of an arbitrary bit stream. There is a limit to how close in time flux transitions can be for reading equipment to detect them, and that constrains how closely bits can be recorded on the medium: In the worst case, with an arbitrary bit stream, there are two consecutive 1's, which produces two consecutive flux transitions in time, so bits must be spaced far enough apart that there would be sufficient time between those flux transitions for the reader to detect them. But this code imposes a constraint of d=1, i.e. there is a minimum of one 0 between each two 1's. That means in the worst case, flux transitions are two bit times apart, so the bits can be twice as close together as with the arbitrary bit stream without exceeding the reader's capabilities.
This doubled recording density compensates for the 1/2 coding rate of this code (it takes two bits to represent one bit of real information) and makes it equivalent to a rate-1 code.
| Data | Encoded |
|---|---|
| 0 | x0 |
| 1 | 01 |
Where "x" is the complement of the previous data bit (which is also the previous encoded bit). Except for the clock bits—that "x" bit, and the "0" in the "01" code—this is the same as the FM table, and that is how this code gets its name. The inserted clock bits are 0 except between two 0 data bits.
Example:
Data: 0 0 1 0 1 1 0 1 0 0 0 1 1 0 Encoded: x010010001010001001010010100 Clock: x 1 0 0 0 0 0 0 0 1 1 0 0 0
(1,7) RLL
(1,7) RLL maps 2 bits of data onto three bits on the disk, and the encoding is done in two or four bit groups. The encoding rules are: (x, y) becomes (NOT x, x AND y, NOT y), except (x, 0, 0, y) becomes (NOT x, x AND y, NOT y, 0, 0, 0).[6] When encoding according to the table below, the longest (last in the table) match must be used; those are exceptions which handle situations where applying the earlier rules would lead to a violation of the code constraints.
| Data | Encoded |
|---|---|
| 00 | 101 |
| 01 | 100 |
| 10 | 001 |
| 11 | 010 |
| 00 00 | 101 000 |
| 00 01 | 100 000 |
| 10 00 | 001 000 |
| 10 01 | 010 000 |
Example:
Data: 0 0 1 0 1 1 0 1 0 0 0 1 1 0 Encoded: 101 001 010 100 100 000 001
(2,7) RLL
(2,7) RLL maps n bits of data onto 2n bits on the disk, but the encoding can be done in two, three or four bit groups.
Western Digital WD5010A, WD5011A, WD50C12
| Data | (2,7) RLL Encoded |
|---|---|
| 11 | 1000 |
| 10 | 0100 |
| 000 | 100100 |
| 010 | 000100 |
| 011 | 001000 |
| 0011 | 00001000 |
| 0010 | 00100100 |
Seagate ST11R
| Data | (2,7) RLL Encoded |
|---|---|
| 11 | 1000 |
| 10 | 0100 |
| 000 | 000100 |
| 010 | 100100 |
| 011 | 001000 |
| 0011 | 00001000 |
| 0010 | 00100100 |
Example:
Data: 1 1 0 1 1 0 0 1 1 Encoded: 1000 001000 00001000
DC Free (1,7) RLL
There is also an alternate (1,7) RLL encoding that is sometimes used to avoid a DC bias (which helps when sending a signal over a long distance or with some types of recording media).
| Data | Encoded |
|---|---|
| 00 | x01 |
| 01 | 010 |
| 10 | x00 |
| 11 00 | 010 001 |
| 11 01 | x00 000 |
| 11 10 | x00 001 |
| 11 11 | 010 000 |
Where "x" is the complement of the previous encoded bit (i.e. 1 if the previous bit was 0, and 0 if the previous bit was 1).
Example:
Data: 0 1 0 0 1 1 0 1 0 1 Encoded: 010 101 000 000 010
HHH(1,13)
The HHH(1,13) code is a rate-2/3 code developed by three IBM researchers (Hirt, Hassner, and Heise) for use in the 16 MB/s IrDA VFIR physical layer.[7] Unlike magnetic encoding, this is designed for an infrared transmitter where a 0 bit represents "off" and a 1 bit represents "on". Because 1 bits consume more power to transmit, this is designed to limit the density of 1 bits to less than 50%. In particular, it is a (1,13|5) RLL code, where the final 5 indicates the additional constraint that there are at most 5 consecutive "10" bit pairs.
| Data | Encoded |
|---|---|
| 00 | 010 |
| 01 | 001 |
| 10 | 100 |
| 11 | 101 |
| 01 10 | 001 000 |
| 01 11 | 010 000 |
| 11 10 | 101 000 |
| 11 11 | 100 000 |
| 00 11 00 | 010 000 000 |
| 00 11 01 | 001 000 000 |
| 10 11 00 | 100 000 000 |
| 10 11 01 | 101 000 000 |
| 00 11 10 11 | 010 000 000 000 |
| 10 11 10 11 | 100 000 000 000 |
The first eight rows describe a standard (1,7)-RLL code. The additional six exceptions increase the maximum run of zeros to 13 (in the legal pattern 100 000 000 000 001, which represents 10 11 10 11, followed by 01), but limit the maximum average ones density to 1⁄3. The longest run of 1–0 pairs is 000 101 010 101 000.
This code limits the ones density to between 1⁄12 and 1⁄3, with an average of 25.8%.
Examples
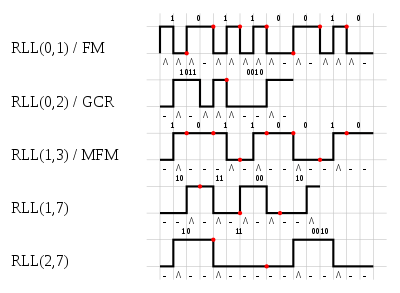
For example let us encode the bit sequence 10110010 with different encodings
| Encoding | Data | Encoded |
|---|---|---|
| RLL(0,1) | 10110010 | 1110111110101110 |
| RLL(0,2) | 1011 0010 | 01011 10010 |
| RLL(1,3) | 10110010 | 0100010100100100 |
| RLL(1,7) | 10 11 00 10 | 001 010 101 001 |
| RLL(2,7) | 10 11 0010 | 0100 1000 00100100 |
Densities
Suppose a magnetic tape can contain up to 3,200 flux reversals per inch. A Modified Frequency Modulation or (1,3) RLL encoding stores each data bit as two bits on tape, but since there is guaranteed to be one 0 (non flux reversal) bit between any 1 (flux reversal) bits then it is possible to store 6,400 encoded bits per inch on the tape, or 3,200 data bits per inch. A (1,7) RLL encoding can also store 6,400 encoded bits per inch on the tape, but since it only takes 3 encoded bits to store 2 data bits this is 4,267 data bits per inch. A (2,7) RLL encoding takes 2 encoded bits to store each data bit, but since there is guaranteed to be two 0 bits between any 1 bits then it is possible to store 9,600 encoded bits per inch on the tape, or 4,800 data bits per inch.
The flux reversal densities on hard drives are significantly greater, but the same improvements in storage density are seen by using different encoding systems.
See also
- 8b/10b encoding
- Bit slip
- Eight-to-fourteen modulation and EFMplus are DC-free (2,10) RLL codes used on CDs and DVDs, respectively.
- Error correcting codes
- Line code
- Modulation
- Physical layer
- PRML
- Run-length encoding
- Self-synchronizing code and bit synchronization
- Source coding
References
This article is based on material taken from the Free On-line Dictionary of Computing prior to 1 November 2008 and incorporated under the "relicensing" terms of the GFDL, version 1.3 or later.
- ↑ A Quarter Century of Disk File Innovation, IBM Journal of Research and Development.
- ↑ P.A. Franaszek (1972), “Run-Length-Limited Variable Length Coding with Error Propagation Limitation”, U.S. Patent 3,689,899.
- ↑ Five decades of disk drive industry firsts, DISK/TREND, Inc., publisher of market studies of the worldwide disk drive and data storage industries. web.archive.org
- ↑ Kees A. Schouhamer Immink. "'Runlength-Limited Sequences', Proceedings IEEE, vol. 78, no. 11, pp. 1745-1759, Nov. 1990.". Retrieved 2015-08-23.
- ↑ Kees A. Schouhamer Immink. "Codes for Mass Data Storage Systems, Second fully revised edition, Shannon Foundation Publishers, Eindhoven, The Netherlands, Nov. 2004. ISBN 90-74249-27-2.". Retrieved 2015-08-23.
- ↑ Mee, C. Denis; Daniel, Eric D. (1996). Magnetic Storage Handbook, 2nd Edition. McGraw Hill. ISBN 0-07-041275-8.
- ↑ Hirt, Walter; Hassner, Martin; Heise, Nyles (February 2001), "IrDA-VFIr (16 Mb/s): modulation code and system design", IEEE Personal Communications, 8 (1): 58–71, doi:10.1109/98.904900