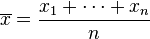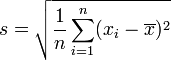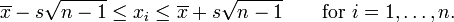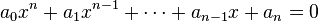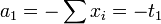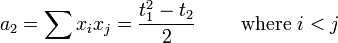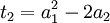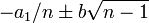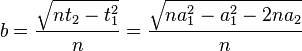Samuelson's inequality
In statistics, Samuelson's inequality, named after the economist Paul Samuelson,[1] also called the Laguerre–Samuelson inequality,[2] after the mathematician Edmond Laguerre, states that every one of any collection x1, ..., xn, is within √(n − 1) sample standard deviations of their sample mean.
Definition
If we let
be the sample mean and
be the standard deviation of the sample, then
Equality holds on the left if and only if the n − 1 smallest of the n numbers are equal to each other, and on the right iff the n − 1 largest ones are equal.
Samuelson's inequality may be considered a reason why studentization of residuals should be done externally.
Relationship to polynomials
Samuelson was not the first to describe this relationship. The first to discover this relationship was probably Laguerre in 1880 while investigating the roots (zeros) of polynomials.[4][5]
Consider a polynomial with all roots real:
Without loss of generality let 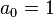 and let
and let
-
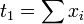 and
and 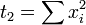
Then
and
In terms of the coefficients
Laguerre showed that the roots of this polynomial were bounded by
where
Inspection shows that 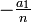 is the mean of the roots and that b is the standard deviation of the roots.
is the mean of the roots and that b is the standard deviation of the roots.
Laguerre failed to notice this relationship with the means and standard deviations of the roots being more interested in the bounds themselves. This relationship permits a rapid estimate of the bounds of the roots and may be of use in their location.
Note
When the coefficients 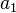 and
and 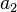 are both zero no information can be obtained about the location of the roots, because not all roots are real (as can be seen from Descartes' rule of signs) unless the constant term is also zero.
are both zero no information can be obtained about the location of the roots, because not all roots are real (as can be seen from Descartes' rule of signs) unless the constant term is also zero.
References
- ↑ Paul Samuelson, "How Deviant Can You Be?", Journal of the American Statistical Association, volume 63, number 324 (December, 1968), pp. 1522–1525 JSTOR 2285901
- ↑ Jensen, Shane Tyler (1999) The Laguerre–Samuelson Inequality with Extensions and Applications in Statistics and Matrix Theory MSc Thesis. Department of Mathematics and Statistics, McGill University.
- ↑ Advances in Inequalities from Probability Theory and Statistics, by Neil S. Barnett and Sever Silvestru Dragomir, Nova Publishers, 2008, page 164
- ↑ Jensen, Shane Tyler (1999) The Laguerre–Samuelson Inequality with Extensions and Applications in Statistics and Matrix Theory MSc Thesis. Department of Mathematics and Statistics, McGill University
- ↑ Laguerre E. (1880) Mémoire pour obtenir par approximation les racines d'une équation algébrique qui a toutes les racines réelles. Nouv Ann Math 2e série, 19, 161–172, 193–202