Quotient of an abelian category
In mathematics, the quotient of an abelian category A by a Serre subcategory B is the category whose objects are those of A and whose morphisms from X to Y are given by the direct limit  over subobjects
over subobjects 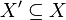 and
and 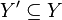 such that
such that 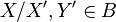 . The quotient A/B will then be an Abelian category, and there is a canonical functor
. The quotient A/B will then be an Abelian category, and there is a canonical functor 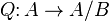 sending an object X to itself and a morphism
sending an object X to itself and a morphism 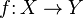 to the corresponding element of the direct limit with X'=X and Y'=0. This Abelian quotient satisfies the universal property that if C is any other Abelian category, and
to the corresponding element of the direct limit with X'=X and Y'=0. This Abelian quotient satisfies the universal property that if C is any other Abelian category, and  is an exact functor such that F(b) is a zero object of C for each
is an exact functor such that F(b) is a zero object of C for each 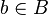 , then there is a unique exact functor
, then there is a unique exact functor 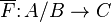 such that
such that 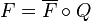 .[1]
.[1]
References
- ↑ Gabriel, Pierre, Des categories abeliennes, Bull. Soc. Math. France 90 (1962), 323-448.
This article is issued from Wikipedia - version of the 12/24/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.