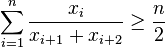Shapiro inequality
In mathematics, the Shapiro inequality is an inequality proposed by H. Shapiro in 1954.
Statement of the inequality
Suppose n is a natural number and 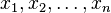 are positive numbers and:
are positive numbers and:
- n is even and less than or equal to 12, or
- n is odd and less than or equal to 23.
Then the Shapiro inequality states that
where 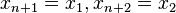 .
.
For greater values of n the inequality does not hold and the strict lower bound is 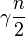 with
with 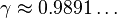 .
.
The initial proofs of the inequality in the pivotal cases n = 12 (Godunova and Levin, 1976) and n = 23 (Troesch, 1989) rely on numerical computations. In 2002, P.J. Bushell and J.B. McLeod published an analytical proof for n = 12.
The value of γ was determined in 1971 by Vladimir Drinfeld, who won a Fields Medal in 1990. Specifically, Drinfeld showed that the strict lower bound γ is given by 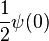 , where ψ is the function convex hull of f(x) = e−x and
, where ψ is the function convex hull of f(x) = e−x and 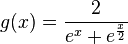 . (That is, the region above the graph of ψ is the convex hull of the union of the regions above the graphs of f and g.)
. (That is, the region above the graph of ψ is the convex hull of the union of the regions above the graphs of f and g.)
Interior local mimima of the left-hand side are always ≥ n/2 (Nowosad, 1968).
Counter-examples for higher n
The first counter-example was found by Lighthill in 1956, for n = 20:
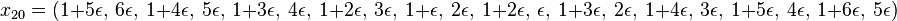 where
where  is close to 0.
is close to 0.
Then the left-hand side is equal to 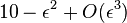 , thus lower than 10 when
, thus lower than 10 when  is small enough.
is small enough.
The following counter-example for n = 14 is by Troesch (1985):
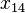 = (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)
= (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)
References
- Fink, A.M. (1998). "Shapiro's inequality". In Gradimir V. Milovanović, G. V. Recent progress in inequalities. Dedicated to Prof. Dragoslav S. Mitrinović. Mathematics and its Applications (Dordrecht) 430. Dordrecht: Kluwer Academic Publishers. pp. 241–248. ISBN 0-7923-4845-1. Zbl 0895.26001.
- Bushell, P.J.; McLeod, J.B. (2002). "Shapiro's cyclic inequality for even n" (PDF). J. Inequal. Appl. 7 (3): 331–348. ISSN 1029-242X. Zbl 1018.26010. They give an analytic proof of the formula for even n ≤ 12, from which the result for all n ≤ 12 follows. They state n = 23 as an open problem.
External links
- Usenet discussion in 1999 (Dave Rusin's notes)
- PlanetMath