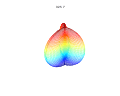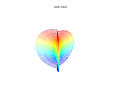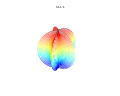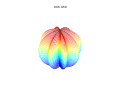Superformula
The superformula is a generalization of the superellipse and was proposed by Johan Gielis around 2000.[1] Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Gielis holds a patent related to the synthesis of patterns generated by the superformula.[2]
In polar coordinates, with the radius and the angle, the superformula is:
By choosing different values for the parameters and different shapes can be generated.
The formula was obtained by generalizing the superellipse, named and popularized by Piet Hein, a Danish mathematician.
Extension to higher dimensions
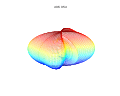
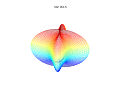
It is possible to extend the formula to 3, 4, or n dimensions, by means of the spherical product of superformulas. For example, the 3D parametric surface is obtained by multiplying two superformulas r1 and r2. The coordinates are defined by the relations:
where (latitude) varies between −π/2 and π/2 and θ (longitude) between −π and π.
Generalization
The superformula can be generalized by replacing the parameter with y and with z:[3]
This allows the creation of rotationally asymmetric and nested structures. In the following examples a, b, and are 1:

Plots
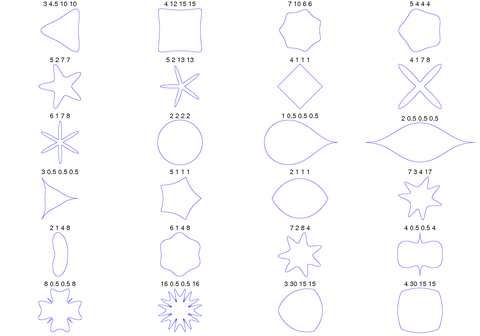
A GNU Octave program for generating these figures:
function sf2d(n, a)
u = [0:.001:2 * pi];
raux = abs(1 / a(1) .* abs(cos(n(1) * u / 4))) .^ n(3) + abs(1 / a(2) .* abs(sin(n(1) * u / 4))) .^ n(4);
r = abs(raux) .^ (- 1 / n(2));
x = r .* cos(u);
y = r .* sin(u);
plot(x, y);
end
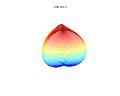
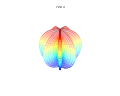
3D superformula: a = b = 1; = = m, n1, n2 and n3 are shown in the pictures.
A GNU Octave program for generating these figures:
function sf3d(n, a)
u = [- pi:.05:pi];
v = [- pi / 2:.05:pi / 2];
nu = length(u);
nv = length(v);
for i = 1:nu
for j = 1:nv
raux1 = abs(1 / a(1) * abs(cos(n(1) .* u(i) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * u(i) / 4))) .^ n(4);
r1 = abs(raux1) .^ (- 1 / n(2));
raux2 = abs(1 / a(1) * abs(cos(n(1) * v(j) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * v(j) / 4))) .^ n(4);
r2 = abs(raux2) .^ (- 1 / n(2));
x(i, j) = r1 * cos(u(i)) * r2 * cos(v(j));
y(i, j) = r1 * sin(u(i)) * r2 * cos(v(j));
z(i, j) = r2 * sin(v(j));
endfor;
endfor;
mesh(x, y, z);
endfunction;
References
- ↑ Gielis, Johan (2003), "A generic geometric transformation that unifies a wide range of natural and abstract shapes", American Journal of Botany, 90 (3): 333–338, doi:10.3732/ajb.90.3.333, ISSN 0002-9122
- ↑ EP patent 1177529, Gielis, Johan, "Method and apparatus for synthesizing patterns", issued 2005-02-02
- ↑
- Stöhr, Uwe (2004), SuperformulaU (PDF)
External links
| Wikimedia Commons has media related to Superformula. |
- Website with information about the superformula and Johan Gielis
- Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization
- Least Squares Fitting of Chacón-Gielis Curves By the Particle Swarm Method of Optimization
- Superformula 2D Plotter & SVG Generator
- Interactive example using JSXGraph
- 3D Superdupershape Explorer using Processing
- Interactive 3D Superformula plotter using Processing (with code)
- SuperShaper: An OpenSource, OpenCL accelerated, interactive 3D SuperShape generator with shader based visualisation (OpenGL3)
- Simpel, WebGL based SuperShape implementation
- The Gielis Supershape Formula, Provides an interactive Java applet for exploring the variety of different shapes, natural or mathematical, that can be formed with the formula.