Ultimate tic-tac-toe

The board of an incomplete Ultimate Tic Tac Toe game

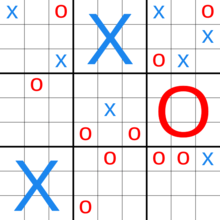
Ultimate tic-tac-toe also known as super tic-tac-toe is a board game composed of nine tic-tac-toe boards arranged in a 3-by-3 grid.^[1] Players take turns playing in the smaller tic-tac-toe boards until one of them wins in the larger tic-tac-toe board. Strategy in this game is much more conceptually difficult, and even proves a challenge for computers!^[2]

Since X played in the top-right corner of the local board, O is forced to play in the top-right local board.

Neither player wins because there are no legal moves left, and neither player managed to win the global board.

Rules

While explaining the rules, each small 3-by-3 tic-tac-toe board will be referred to as a local board, and the larger 3-by-3 board will be referred to as the global board.

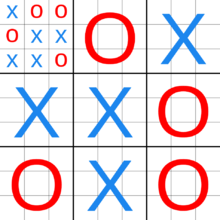
The game starts with X playing wherever he wants in any of the 81 empty spots. This move 'sends' the next player to its relative location. For example, if X played in the middle of his local board, then O needs to play next in the local board in the middle of the global board. This game rule is easier to understand from the second image, where X played in the top-right corner of the central local board, forcing O (red) to play in the top-right local board. O can then play in any one of the nine available spots in the top-right local board, each move sending X to a different local board.

Note that if a player is sent to an already completed local board (either won by either player or tied), then that player may play wherever it wants (as long as the move is legal).

If a move is played so that it is to win a local board by the rules of normal tic-tac-toe, then it wins that local board. Game play ends when either a player wins the global board, or there are no legal moves remaining.^[2]

X played in the top-center of the local board, sending O to the top-center local board. However, since that board cannot be played in (in this case it's already won), O can play wherever it wants (assuming the move is legal).

X wins since it won the global tic-tac-toe board.

Gameplay

Ultimate tic-tac-toe is significantly more complex than most other variations of tic-tac-toe, as there is no clear strategy to playing. This is because of the complicated game branching in this game. Even though every move must be played in a local board, equivalent to a normal tic-tac-toe board, each move must take into account the global board in several ways:

1. Anticipating the next move: Each move played in a local board determines where the opponent's next move may be played. This might make moves that may be considered bad in normal tic-tac-toe viable, since the opponent is sent to another local board, and may be unable to immediately respond to them. Therefore, players are forced to consider the larger game board instead of simply focusing on the local board.
2. Visualizing the game tree: Visualizing future branches of the game tree is also much more difficult. Each move determines the next move, and therefore reading ahead—predicting future moves—follows a much less linear path. Future board positions are no longer interchangeable, each move leading to starkly different possible future positions. This makes the game tree far more difficult to visualize, leaving many possible paths overlooked.
3. Winning the game: Due to the rules of ultimate tic-tac-toe, the global board is never directly effected. It is only governed by actions that occur in local boards. This means that each local move played is not intended to win the local board, yet to win the global board. Local wins are not valuable if they cannot be used to win the global board—in fact, it may be strategic to sacrifice a local board to your opponent in order to win a more important local board yourself. This added layer of complexity makes it much harder for humans to analyze the relative importance and significance of moves, and consequently much harder to play well.

Computer implementations

While tic-tac-toe is elementary to solve, and can be done nearly instantly using depth-first search, ultimate tic-tac-toe cannot be reasonably solved using any brute force tactics.^[3] Therefore, more creative computer implementations are necessary in order to play this game.

The most common artificial intelligence (AI) tactic, minimax, may be used to play ultimate tic-tac-toe, but has difficulty playing this. This is because, despite having relatively simple rules, ultimate tic-tac-toe lacks any simple heuristic evaluation function. This function is necessary in minimax, for it determines how good a specific position is. Although elementary evaluation functions can be made for ultimate tic-tac-toe by taking into account the number of local victories, these largely overlook positional advantage that is much harder to quantify. Without any efficient evaluation function, most typical computer implementations are weak, and therefore there are few computer opponents that can consistently outplay humans.

However, artificial intelligence algorithms that don't need evaluation functions, like the Monte Carlo tree-search algorithm, have no problem in playing this game. The Monte Carlo tree-search relies on random simulations of games in order to determine how good a position is instead of a positional evaluation, and is therefore able to accurately access how good a current position is. Therefore, computer implementations using these algorithms tend to outperform minimax solutions, and can consistently beat human opponents.^[4]

References

1. Whitney, George; Janoski, Janine (November 26, 2016). "Group Actions on Winning Games of Super Tic-Tac-Toe" (PDF).
2. Orlin, Ben (2013-06-16). "Ultimate Tic-Tac-Toe". Math with Bad Drawings. Retrieved 2016-10-18.
3. Schaefer, Steve (2002). "MathRec Solutions (Tic-Tac-Toe)". Retrieved 2016-10-18.
4. Gila, Ofek (2016-06-27). "What is the Monte Carlo tree search?". We Blog. Retrieved 2016-10-18.

External Links

• Detailed explanation from Math with Bad Drawings
• Strong Monte Carlo tree-search implementation