Zubov's method
Zubov's method is a technique for computing the basin of attraction for a set of ordinary differential equations (a dynamical system). The domain of attraction is the set 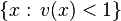 , where
, where 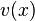 is the solution to a partial differential equation known as the Zubov equation. 'Zubov's method' can be used in a number of ways.
is the solution to a partial differential equation known as the Zubov equation. 'Zubov's method' can be used in a number of ways.
Zubov's theorem states that:
- If
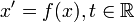 is an ordinary differential equation in
is an ordinary differential equation in 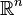 with
with 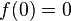 , a set
, a set  containing 0 in its interior is the domain of attraction of zero if and only if there exist continuous functions
containing 0 in its interior is the domain of attraction of zero if and only if there exist continuous functions 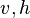 such that:
such that:
-
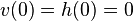 ,
, 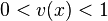 for
for 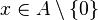 ,
, 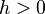 on
on 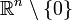
- for every
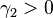 there exist
there exist 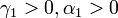 such that
such that 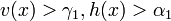 , if
, if 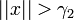
-
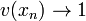 for
for 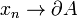 or
or 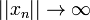
-
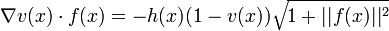
-
If f is continuously differentiable, then the differential equation has at most one continuously differentiable solution satisfying 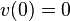 .
.
References
Vladimir Ivanovich Zubov, Methods of A.M. Lyapunov and their application, Izdatel'stvo Leningradskogo Universiteta, 1961. (Translated by the United States Atomic Energy Commission, 1964.) ASIN B0007F2CDQ.
This article is issued from Wikipedia - version of the 10/6/2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.