Epsilon-induction

In mathematics, 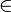$\in$-induction (epsilon-induction) is a variant of transfinite induction that can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets. In symbols:

$\forall x \Big(\forall y (y \in x \rightarrow P[y]) \rightarrow P[x]\Big) \rightarrow \forall x \, P[x]$

This principle, sometimes called the axiom of induction (in set theory), is equivalent to the axiom of regularity given the other ZF axioms. 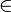$\in$-induction is a special case of well-founded induction.

The name is most often pronounced "epsilon-induction", because the set membership symbol 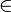$\in$ historically developed from the Greek letter $\epsilon$.

See also

• Mathematical induction
• Transfinite induction
• Well-founded induction