Augmented seventh
| Inverse | diminished second |
|---|---|
| Name | |
| Other names | - |
| Abbreviation | A7[1] |
| Size | |
| Semitones | 12 |
| Interval class | 0 |
| Just interval | 125:64[2] |
| Cents | |
| Equal temperament | 1200 |
| 24 equal temperament | 1150 |
| Just intonation | 1159 |
Play equal temperament or Just .
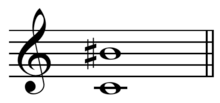
Play In classical music from Western culture, an augmented seventh is an interval produced by widening a major seventh by a chromatic semitone. For instance, the interval from C to B is a major seventh, eleven semitones wide, and both the intervals from C♭ to B, and from C to B♯ are augmented sevenths, spanning twelve semitones. Being augmented, it is classified as a dissonant interval.[3] However, it is enharmonically equivalent to the perfect octave.
Since an octave can be described as a major seventh augmented by a diatonic semitone, the augmented seventh is the sum of an octave, plus the difference between the chromatic and diatonic semitones, which makes it a highly variable quantity between one meantone tuning and the next. In standard equal temperament, in fact, it is identical to the perfect octave ( Play ), because both semitones have the same size. In 19 equal temperament, on the other hand, the interval is 63 cents short of an octave, i.e. 1137 cents. More typical meantone tunings fall between these extremes, giving it an intermediate size.
In just intonation, three major thirds in succession make up an augmented seventh, which is just short of an octave by 41.05 cents. Adding a diesis to this makes up an octave. Hence, this interval's complement, the diminished second, is often referred to as a diesis.
See also
Sources
- ↑ Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.54. ISBN 978-0-07-294262-0. Specific example of an A7 not given but general example of major intervals described.
- ↑ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxvi. ISBN 0-8247-4714-3. Classic augmented seventh.
- ↑ Benward & Saker (2003), p.92.