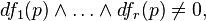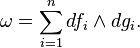Carathéodory–Jacobi–Lie theorem
The Carathéodory–Jacobi–Lie theorem is a theorem in symplectic geometry which generalizes Darboux's theorem.
Statement
Let M be a 2n-dimensional symplectic manifold with symplectic form ω. For p ∈ M and r ≤ n, let f1, f2, ..., fr be smooth functions defined on an open neighborhood V of p whose differentials are linearly independent at each point, or equivalently
where {fi, fj} = 0. (In other words they are pairwise in involution.) Here {–,–} is the Poisson bracket. Then there are functions fr+1, ..., fn, g1, g2, ..., gn defined on an open neighborhood U ⊂ V of p such that (fi, gi) is a symplectic chart of M, i.e., ω is expressed on U as
Applications
As a direct application we have the following. Given a Hamiltonian system as 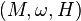 where M is a symplectic manifold with symplectic form
where M is a symplectic manifold with symplectic form 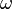 and H is the Hamiltonian function, around every point where
and H is the Hamiltonian function, around every point where 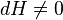 there is a symplectic chart such that one of its coordinates is H.
there is a symplectic chart such that one of its coordinates is H.
References
- Lee, John M., Introduction to Smooth Manifolds, Springer-Verlag, New York (2003) ISBN 0-387-95495-3. Graduate-level textbook on smooth manifolds.