Clubsuit
In mathematics, and particularly in axiomatic set theory, ♣S (clubsuit) is a family of combinatorial principles that are weaker version of the corresponding ◊S; it was introduced in 1975 .
Definition
For a given cardinal number 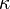 and a stationary set
and a stationary set 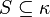 ,
, 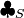 is the statement that there is a sequence
is the statement that there is a sequence 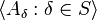 such that
such that
- every Aδ is a cofinal subset of δ
- for every unbounded subset
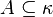 , there is a
, there is a 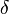 so that
so that 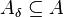
 is usually written as just
is usually written as just 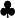 .
.
♣ and ◊
It is clear that ◊ ⇒ ♣, and it was shown in 1975 that ♣ + CH ⇒ ◊; however, Saharon Shelah gave a proof in 1980 that there exists a model of ♣ in which CH does not hold, so ♣ and ◊ are not equivalent (since ◊ ⇒ CH).
References
- A. J. Ostaszewski, On countably compact perfectly normal spaces, Journal of London Mathematical Society, 1975 (2) 14, pp. 505-516.
- S. Shelah, Whitehead groups may not be free, even assuming CH, II, Israel Journal of Mathematics, 1980 (35) pp. 257-285.
See also
This article is issued from Wikipedia - version of the 4/12/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.