Discontinuity layout optimization

Failure mechanism of an embedded foundation (identified using DLO)

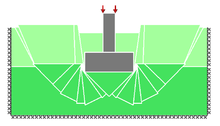
Discontinuity layout optimization (DLO) is an engineering analysis procedure which can be used to directly establish the amount of load that can be carried by a solid or structure prior to collapse. Using DLO the layout of failure planes, or 'discontinuities', in a collapsing solid or structure are identified using mathematical optimization methods (hence the name, 'discontinuity layout optimization'). It is assumed that failure occurs in a ductile or 'plastic' manner.

How it works

The DLO procedure involves a number of steps, as outlined below.

The set of potential discontinuities can include discontinuities which crossover one another, allowing complex failure patterns to be identified (e.g. involving ‘fan’ mechanisms, where many discontinuities radiate from a point).

DLO can be formulated in terms of equilibrium relations ('static' formulation) or in terms of displacements ('kinematic' formulation). In the latter case the objective of the mathematical optimization problem is to minimize the internal energy dissipated along discontinuities, subject to nodal compatibility constraints. This can be solved using efficient linear programming techniques and, when combined with an algorithm originally developed for truss layout optimization problems,^[1] it has been found that modern computer power can be used to directly search through very large numbers of different failure mechanism topologies (up to approx. 2^{1,000,000,000} different topologies on current generation PCs). A full description of the application of DLO to plane strain problems has been provided by Smith and Gilbert,^[2] to masonry arch analysis by Gilbert et al,^[3] to slab problems by Gilbert et al,^{[4] [5]} and to 3D problems by Hawksbee et al,^[6] and Zhang.^[7]

DLO vs FEM

Whereas with finite element analysis (FEM), a widely used alternative engineering analysis procedure, mathematical relations are formed for the underlying continuum mechanics problem, DLO involves analysis of a potentially much simpler discontinuum problem, with the problem being posed entirely in terms of the individual discontinuities which interconnect nodes laid out across the body under consideration. Additionally, when general purpose finite element programs are used to analyse the collapse state often relatively complex non-linear solvers are required, in contrast to the simpler linear programming solvers generally required in the case of DLO.

Compared with non-linear FEM, DLO has the following advantages and disadvantages:

Advantages

• The collapse state is analysed directly, without the need to iterate. This means that solutions can generally be obtained much more quickly.
• The output, in the form of animated failure mechanisms is generally easier to interpret.
• Problems involving singularities in the stress or displacement fields can be dealt with without difficulty.
• As DLO is much simpler than non-linear FEM, users require less training in order to use the method effectively.

Disadvantages

• As with other limit analysis techniques, DLO provides no information about displacements (or stresses) prior to collapse.
• DLO is fundamentally based in modelling compatible mechanisms for soil collapse and is therefore an upper bound method. As a result, the method will always predict an unconservative collapse load.
• Although the discontinuity layout generation and linear programming optimization schemes used in DLO will usually ensure that a good approximation of the true collapse mechanism is found, there is no way of discerning by how much the predicted collapse load will exceed the true collapse load without comparison to an independent lower bound analysis.
• DLO is a relatively new technique so only a limited range of software tools are currently available.

Applications

DLO is perhaps most usefully applied to engineering problems where traditional hand calculations are difficult, or simplify the problem too much, but where recourse to more complex non-linear FEM is not justified. Applications include:

• Analysis of geotechnical engineering problems (e.g. slope stability, bearing capacity^[8] or retaining wall problems).
• Analysis of concrete slab problems.
• Analysis of metal forming or extrusion problems.

Software using Discontinuity Layout Optimization

• MATLAB script (2009-) Provided by the CMD research group at the University of Sheffield, UK.
• LimitState:GEO (2008-) General purpose geotechnical software application.
• LimitState:SLAB (2015-) Slab analysis software application.

References

1. Gilbert, M. and Tyas, A. (2003) Layout optimization of large-scale pin-jointed frames, Engineering Computations, Vol. 20, No. 8, pp.1044-1064
2. Smith, C.C. and Gilbert, M. (2007) Application of discontinuity layout optimization to plane plasticity problems, Proc. Royal Society A, Volume 463, Number 2086, pp.2461-2484.
3. Gilbert, M., Smith, C.C. and Pritchard, T.J. (2010) Masonry arch analysis using discontinuity layout optimisation. ICE-Engineering and Computational Mechanics, Volume 163, pp.167-178.
4. Gilbert, M., He, L., Smith, C.C. and Le, C.V. (2014) Automatic yield-line analysis of slabs using discontinuity layout optimization. Proceedings Royal Society A, Volume 470, paper 20140071.
5. He, L. and Gilbert, M. (2016) Automatic rationalization of yield-line patterns identified using discontinuity layout optimization. International Journal of Solids and Structures, Volume 84, pp.27-39.
6. Hawksbee, S., Smith, C.C. and Gilbert, M. (2013) Application of discontinuity layout optimization to three-dimensional plasticity problems. Proceedings Royal Society A, Volume 469, paper 20130009.
7. Zhang, Y. (2016) Multi-slicing strategy for the three-dimensional discontinuity layout optimization (3D DLO). International Journal for Numerical and Analytical Methods in Geomechanics, DOI: 10.1002/nag.2566.
8. Lee, Y.S., Smith C.C. and Cheuk C.Y. (2008) Bearing capacity of embedded foundations. In 2nd International Conference on Foundations, ICOF 2008, Dundee, pp.961-972.

External links

• DLO teaching resources provided by the Geotechnical Engineering Research Group at the University of Sheffield, UK.