Evolutionary algorithm
In artificial intelligence, an evolutionary algorithm (EA) is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions (see also loss function). Evolution of the population then takes place after the repeated application of the above operators. Artificial evolution (AE) describes a process involving individual evolutionary algorithms; EAs are individual components that participate in an AE..
Evolutionary algorithms often perform well approximating solutions to all types of problems because they ideally do not make any assumption about the underlying fitness landscape; this generality is shown by successes in fields as diverse as engineering, art, biology, economics, marketing, genetics, operations research, robotics, social sciences, physics, politics and chemistry.
Techniques from evolutionary algorithms applied to the modeling of biological evolution are generally limited to explorations of microevolutionary processes and planning models based upon cellular processes. The computer simulations Tierra and Avida attempt to model macroevolutionary dynamics.
In most real applications of EAs, computational complexity is a prohibiting factor. In fact, this computational complexity is due to fitness function evaluation. Fitness approximation is one of the solutions to overcome this difficulty. However, seemingly simple EA can solve often complex problems; therefore, there may be no direct link between algorithm complexity and problem complexity.
A possible limitation of many evolutionary algorithms is their lack of a clear genotype-phenotype distinction. In nature, the fertilized egg cell undergoes a complex process known as embryogenesis to become a mature phenotype. This indirect encoding is believed to make the genetic search more robust (i.e. reduce the probability of fatal mutations), and also may improve the evolvability of the organism.[1][2] Such indirect (aka generative or developmental) encodings also enable evolution to exploit the regularity in the environment.[3] Recent work in the field of artificial embryogeny, or artificial developmental systems, seeks to address these concerns. And gene expression programming successfully explores a genotype-phenotype system, where the genotype consists of linear multigenic chromosomes of fixed length and the phenotype consists of multiple expression trees or computer programs of different sizes and shapes.[4]
Implementation of biological processes
Step One: Generate the initial population of individuals randomly. (First generation)
Step Two: Evaluate the fitness of each individual in that population (time limit, sufficient fitness achieved, etc.)
Step Three: Repeat the following regenerational steps until termination:
- Select the best-fit individuals for reproduction. (Parents)
- Breed new individuals through crossover and mutation operations to give birth to offspring.
- Evaluate the individual fitness of new individuals.
- Replace least-fit population with new individuals.
Evolutionary algorithm types
Similar techniques differ in genetic representation and other implementation details, and the nature of the particular applied problem.
- Genetic algorithm – This is the most popular type of EA. One seeks the solution of a problem in the form of strings of numbers (traditionally binary, although the best representations are usually those that reflect something about the problem being solved), by applying operators such as recombination and mutation (sometimes one, sometimes both). This type of EA is often used in optimization problems. Another name for it is fetura, from the Latin for breeding[5].
- Genetic programming – Here the solutions are in the form of computer programs, and their fitness is determined by their ability to solve a computational problem.
- Evolutionary programming – Similar to genetic programming, but the structure of the program is fixed and its numerical parameters are allowed to evolve.
- Gene expression programming – Like genetic programming, GEP also evolves computer programs but it explores a genotype-phenotype system, where computer programs of different sizes are encoded in linear chromosomes of fixed length.
- Evolution strategy – Works with vectors of real numbers as representations of solutions, and typically uses self-adaptive mutation rates.
- Differential evolution – Based on vector differences and is therefore primarily suited for numerical optimization problems.
- Neuroevolution – Similar to genetic programming but the genomes represent artificial neural networks by describing structure and connection weights. The genome encoding can be direct or indirect.
- Learning classifier system – Here the solution is a set of classifiers (rules or conditions). A Michigan-LCS evolves at the level of individual classifiers whereas a Pittsburgh-LCS uses populations of classifier-sets. Initially, classifiers were only binary, but now include real, neural net, or S-expression types. Fitness is typically determined with either a strength or accuracy based reinforcement learning or supervised learning approach.
Related techniques
Swarm algorithms, including:
- Ant colony optimization – Based on the ideas of ant foraging by pheromone communication to form paths. Primarily suited for combinatorial optimization and graph problems.
- The runner-root algorithm (RRA) is inspired by the function of runners and roots of plants in nature [6]
- Artificial bee colony algorithm – Based on the honey bee foraging behaviour. Primarily proposed for numerical optimization and extended to solve combinatorial, constrained and multi-objective optimization problems.
- Bees algorithm is based on the foraging behaviour of honey bees. It has been applied in many applications such as routing and scheduling.
- Cuckoo search is inspired by the brooding parasitism of the cuckoo species. It also uses Lévy flights, and thus it suits for global optimization problems.
- Particle swarm optimization – Based on the ideas of animal flocking behaviour. Also primarily suited for numerical optimization problems.
Other population-based metaheuristic methods
- Hunting Search - A method inspired by group hunting of some animals such as wolves that organize their position to surround the prey, each of them is relative to the position of the others and especially in relation to the position of their leader. It is a continuous optimization method [7] adapted as a combinatorial optimization method.[8]
- Adaptive dimensional search – Adaptive dimensional search algorithm differs from nature-inspired metaheuristic techniques in the sense that it does not use any metaphor as an underlying principle for its implementation. Rather it utilizes a simple performance-oriented methodology based on the update of the search dimensionality ratio (SDR) parameter at each iterationm.[9]
- Firefly algorithm is inspired by the behavior of fireflies, attracting each other by flashing light. This is especially useful for multimodal optimization.
- Harmony search – Based on the ideas of musicians' behavior in searching for better harmonies. This algorithm is suitable for combinatorial optimization as well as parameter optimization.
- Gaussian adaptation – Based on information theory. Used for maximization of manufacturing yield, mean fitness or average information. See for instance Entropy in thermodynamics and information theory.
- Memetic algorithm – It is the hybrid form of population based methods. Inspired by Dawkins' notion of a meme, it commonly takes the form of a population-based algorithm coupled with individual learning procedures capable of performing local refinements. Emphasizes the exploitation of problem-specific knowledge, and tries to orchestrate local and global search in a synergic way.
See also
- Adaptive dimensional search
- Artificial development
- Developmental biology
- Digital organism
- Estimation of distribution algorithm
- Evolutionary computation
- Evolutionary robotics
- Fitness function
- Fitness landscape
- Fitness approximation
- Genetic operators
- Interactive evolutionary computation
- List of digital organism simulators
- No free lunch in search and optimization
- Program synthesis
- Test functions for optimization
Gallery[10][11]
-
.gif)
A two-population EA search over a constrained Rosenbrock function with bounded global optimum.
-
.gif)
A two-population EA search over a constrained Rosenbrock function. Global optimum is not bounded.
-
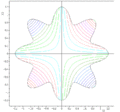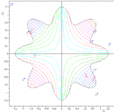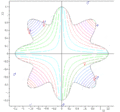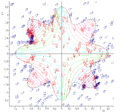
A two-population EA search of a bounded optima of Simionescu's function.
References
- ↑ G.S. Hornby and J.B. Pollack. Creating high-level components with a generative representation for body-brain evolution. Artificial Life, 8(3):223–246, 2002.
- ↑ Jeff Clune, Benjamin Beckmann, Charles Ofria, and Robert Pennock. "Evolving Coordinated Quadruped Gaits with the HyperNEAT Generative Encoding". Proceedings of the IEEE Congress on Evolutionary Computing Special Section on Evolutionary Robotics, 2009. Trondheim, Norway.
- ↑ J. Clune, C. Ofria, and R. T. Pennock, "How a generative encoding fares as problem-regularity decreases," in PPSN (G. Rudolph, T. Jansen, S. M. Lucas, C. Poloni, and N. Beume, eds.), vol. 5199 of Lecture Notes in Computer Science, pp. 358–367, Springer, 2008.
- ↑ Ferreira, C., 2001. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. Complex Systems, Vol. 13, issue 2: 87–129.
- ↑ Wayward World, by Jon Roland. Novel that uses fetura to select candidates for public office.
- ↑ F. Merrikh-Bayat, The runner-root algorithm: A metaheuristic for solving unimodal and multimodal optimization problems inspired by runners and roots of plants in nature, Applied Soft Computing, Vol. 33, pp. 292–303, 2015
- ↑ R. Oftadeh et al (2010), A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search, 60, 2087–2098.
- ↑ A. Agharghor and M,E. Riffi (2017), First Adaptation of Hunting Search Algorithm for the Quadratic Assignment Problem, 520, 263-267. doi=10.1007/978-3-319-46568-5_27
- ↑ Hasançebi, O., Kazemzadeh Azad, S. (2015), Adaptive Dimensional Search: A New Metaheuristic Algorithm for Discrete Truss Sizing Optimization, Computers and Structures, 154, 1–16.
- ↑ Simionescu, P.A.; Dozier, G.V.; Wainwright, R.L. (2006), A Two-Population Evolutionary Algorithm for Constrained Optimization Problems, Proc 2006 IEEE International Conference on Evolutionary Computation, Portland, OR, pp. 1647–1653, doi:10.1109/CEC.2006.1688506
- ↑ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
Bibliography
- Ashlock, D. (2006), Evolutionary Computation for Modeling and Optimization, Springer, ISBN 0-387-22196-4.
- Bäck, T. (1996), Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms, Oxford Univ. Press.
- Bäck, T., Fogel, D., Michalewicz, Z. (1997), Handbook of Evolutionary Computation, Oxford Univ. Press.
- Banzhaf, W., Nordin, P., Keller, R., Francone, F. (1998), Genetic Programming - An Introduction, Morgan Kaufmann, San Francisco
- Eiben, A.E., Smith, J.E. (2003), Introduction to Evolutionary Computing, Springer.
- Holland, J. H. (1975), Adaptation in Natural and Artificial Systems, The University of Michigan Press, Ann Arbor
- Michalewicz Z., Fogel D.B. (2004). How To Solve It: Modern Heuristics, Springer.
- Benkő A., Dósa G., Tuza Z. (2010), Bin Packing/Covering with Delivery, Solved with the Evolution of Algorithms, Proc. 2010 IEEE 5th International Conference on Bio-Inspired Computing: Theories and Applications, BIC-TA 2010, pp. 298–302.
- Poli, R.; Langdon, W. B.; McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely available from the internet. ISBN 978-1-4092-0073-4.
- Price, K., Storn, R.M., Lampinen, J.A., (2005). "Differential Evolution: A Practical Approach to Global Optimization", Springer.
- Ingo Rechenberg (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
- Hans-Paul Schwefel (1974): Numerische Optimierung von Computer-Modellen (PhD thesis). Reprinted by Birkhäuser (1977).
- Simon, D. (2013): Evolutionary Optimization Algorithms, Wiley.
- Computational Intelligence: A Methodological Introduction by Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer, ISBN 978-1-4471-5012-1
