Letter frequency
The frequency of letters in text has been studied for use in cryptanalysis, and frequency analysis in particular, dating back to the Iraqi mathematician Al-Kindi (c. 801–873 CE), who formally developed the method (the ciphers breakable by this technique go back at least to the Caesar cipher invented by Julius Caesar, so this method could have been explored in classical times).
Letter frequency analysis gained additional importance in Europe with the development of movable type in 1450 CE, where one must estimate the amount of type required for each letterform, as evidenced by the variations in letter compartment size in typographer's type cases.
Linguists use letter frequency analysis as a rudimentary technique for language identification, where it's particularly effective as an indication of whether an unknown writing system is alphabetic, syllablic, or ideographic. For example, the Japanese Hiragana syllabary contains 46 distinct characters, which is more than most phonetic alphabets, e.g. the Hawaiian alphabet which has a mere 13 letters, or English which has 26.
No exact letter frequency distribution underlies a given language, since all writers write slightly differently. However, most languages have a characteristic distribution which is strongly apparent in longer texts. Even language change as extreme as from old English to modern English (regarded as mutually unintelligible) show strong trends in related letter frequencies: over a small sample of Biblical passages, from most frequent to least frequent, enaid sorhm tgþlwu (æ)cfy ðbpxz of old English compares to eotha sinrd luymw fgcbp kvjqxz of modern English, with the most extreme differences concerning letterforms not shared.[1]
Linotype machines (which seem to have been primarily or exclusively marketed for English-language typesetting) assumed the letter order, from most to least common, to be etaoin shrdlu cmfwyp vbgkjq xz based on the experience and custom of manual compositors.
Modern International Morse code (generally believed to have been developed by Alfred Vail based on English-language letter frequencies of the 1830s) encodes the most frequent letters with the shortest symbols; arranging the Morse alphabet into groups of letters that require equal amounts of time to transmit, and then sorting these groups in increasing order, yields e it san hurdm wgvlfbk opxcz jyq. Similar ideas are used in modern data-compression techniques such as Huffman coding.
Letter frequency was used by other telegraph systems, such as the Murray Code.
Introduction
Letter frequencies, like word frequencies, tend to vary, both by writer and by subject. One cannot write an essay about x-rays without using frequent Xs, and the essay will have an idiosyncratic letter frequency if the essay is about the frequent use of x-rays to treat zebras in Qatar. Different authors have habits which can be reflected in their use of letters. Hemingway's writing style, for example, is visibly different from Faulkner's. Letter, bigram, trigram, word frequencies, word length, and sentence length can be calculated for specific authors, and used to prove or disprove authorship of texts, even for authors whose styles are not so divergent.
Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text. With the availability of modern computing and collections of large text corpora, such calculations are easily made. Examples can be drawn from a variety of sources (press reporting, religious texts, scientific texts and general fiction) and there are differences especially for general fiction with the position of 'h' and 'i', with H becoming more common.
Herbert S. Zim, in his classic introductory cryptography text "Codes and Secret Writing", gives the English letter frequency sequence as "ETAON RISHD LFCMU GYPWB VKJXQ Z", the most common letter pairs as "TH HE AN RE ER IN ON AT ND ST ES EN OF TE ED OR TI HI AS TO", and the most common doubled letters as "LL EE SS OO TT FF RR NN PP CC".[2]
Also, to note that different dialects of a language will also affect a letter's frequency. For example, an author in the United States would produce something where the letter 'z' is more common as words like "analyze", "apologize" or "recognize" contain the letter, whereas in British English they do not. This would highly affect the frequency of the letter 'z' as it is a rarely used letter elsewhere in the English language.[3]
The "top twelve" letters constitute about 80% of the total usage. The "top eight" letters constitute about 65% of the total usage. Letter frequency as a function of rank can be fitted well by several rank functions, with the two-parameter Cocho/Beta rank function being the best.[4] Another rank function with no adjustable free parameter also fits the letter frequency distribution reasonably well[5] (the same function has been used to fit the amino acid frequency in protein sequences.[6]) A spy using the VIC cipher or some other cipher based on a straddling checkerboard typically uses a mnemonic such as "a sin to err" (dropping the second "r")[7][8] or "at one sir"[9] to remember the top eight characters.
The use of letter frequencies and frequency analysis plays a fundamental role in cryptograms and several word puzzle games, including Hangman, Scrabble and the television game show Wheel of Fortune. One of the earliest descriptions in classical literature of applying the knowledge of English letter frequency to solving a cryptogram is found in E.A. Poe's famous story The Gold-Bug, where the method is successfully applied to decipher a message instructing on the whereabouts of a treasure hidden by Captain Kidd.[10]
Letter frequencies had a strong effect on the design of some keyboard layouts. The most-frequent letters are on the bottom row of the Blickensderfer typewriter, and the home row of the Dvorak Simplified Keyboard.
Relative frequencies of letters in the English language
.svg.png)
.svg.png)
Analysis of entries in the Concise Oxford dictionary is published by the compilers.[11] The table below is taken from Pavel Mička's website, which cites Robert Lewand's Cryptological Mathematics.[12]
| Letter | Relative frequency in the English language | |
|---|---|---|
| a | 8.167% | |
| b | 1.492% | |
| c | 2.782% | |
| d | 4.253% | |
| e | 12.702% | |
| f | 2.228% | |
| g | 2.015% | |
| h | 6.094% | |
| i | 6.966% | |
| j | 0.153% | |
| k | 0.772% | |
| l | 4.025% | |
| m | 2.406% | |
| n | 6.749% | |
| o | 7.507% | |
| p | 1.929% | |
| q | 0.095% | |
| r | 5.987% | |
| s | 6.327% | |
| t | 9.056% | |
| u | 2.758% | |
| v | 0.978% | |
| w | 2.360% | |
| x | 0.150% | |
| y | 1.974% | |
| z | 0.074% | |
According to Lewand, arranged from most to least common in appearance, the letters are: etaoinshrdlcumwfgypbvkjxqz
This table differs slightly from others, such as Cornell University Math Explorer's Project, which produced a table after measuring 40,000 words.[13]
In English, the space is slightly more frequent than the top letter (e) [14] and the non-alphabetic characters (digits, punctuation, etc.) collectively occupy the fourth position (having already included the space) between t and a.[15]
Relative frequencies of the first letters of a word in the English language
The frequency of the first letters of words or names is helpful in pre-assigning space in physical files and indexes.[16] Given 26 filing cabinet drawers, rather than a 1:1 assignment of one drawer to one letter of the alphabet, it is often useful to use a more equal-frequency-letter code by assigning several low-frequency letters to the same drawer (often one drawer is labeled VWXYZ), and to split up the most-frequent initial letters—S, A, and C -- into several drawers (often 4 drawers Aa-An, Ao-At, Ca-Cj, Ck-Cz, Sa-Si, Sj-Sz). The same system is used in some multi-volume works such as some encyclopedias. Cutter numbers, another mapping of names to a more equal-frequency code, are used in some libraries.
The first letter of an English word, from most to least common, t o a w b c d s f m r h i y e g l n p u j k q z x[17]
Both the overall letter distribution and the word-initial letter distribution approximately match the Zipf distribution and even more closely match the Yule distribution.[18]
Often the frequency distribution of the first digit in each datum is significantly different from the overall frequency of all the digits in a set of numeric data—see Benford's law for details.
Analysis of a subset of Project Gutenberg text which shows the frequencies which various letters are found at the beginnings of words:[19]
| Letter | Relative frequency as the first letter of an English word | |
|---|---|---|
| a | 11.602% | |
| b | 4.702% | |
| c | 3.511% | |
| d | 2.670% | |
| e | 2.007% | |
| f | 3.779% | |
| g | 1.950% | |
| h | 7.232% | |
| i | 6.286% | |
| j | 0.597% | |
| k | 0.590% | |
| l | 2.705% | |
| m | 4.383% | |
| n | 2.365% | |
| o | 6.264% | |
| p | 2.545% | |
| q | 0.173% | |
| r | 1.653% | |
| s | 7.755% | |
| t | 16.671% | |
| u | 1.487% | |
| v | 0.649% | |
| w | 6.753% | |
| x | 0.017% | |
| y | 1.620% | |
| z | 0.034% | |
Relative frequencies of letters in other languages
| Letter | English | French [20] | German [21] | Spanish [22] | Portuguese [23] | Esperanto [24] | Italian [25] | Turkish [26] | Swedish [27] | Polish [28] | Dutch [29] | Danish [30] | Icelandic [31] | Finnish [32] | Czech |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 8.167% | 7.636% | 6.516% | 11.525% | 14.634% | 12.117% | 11.745% | 12.920% | 9.383% | 10.503% | 7.486% | 6.025% | 10.110% | 12.217% | 8.421% |
| b | 1.492% | 0.901% | 1.886% | 2.215% | 1.043% | 0.980% | 0.927% | 2.844% | 1.535% | 1.740% | 1.584% | 2.000% | 1.043% | 0.281% | 0.822% |
| c | 2.782% | 3.260% | 2.732% | 4.019% | 3.882% | 0.776% | 4.501% | 1.463% | 1.486% | 3.895% | 1.242% | 0.565% | 0 | 0.281% | 0.740% |
| d | 4.253% | 3.669% | 5.076% | 5.010% | 4.992% | 3.044% | 3.736% | 5.206% | 4.702% | 3.725% | 5.933% | 5.858% | 1.575% | 1.043% | 3.475% |
| e | 12.702% | 14.715% | 16.396% | 12.181% | 12.570% | 8.995% | 11.792% | 9.912% | 10.149% | 7.352% | 18.91% | 15.453% | 6.418% | 7.968% | 7.562% |
| f | 2.228% | 1.066% | 1.656% | 0.692% | 1.023% | 1.037% | 1.153% | 0.461% | 2.027% | 0.143% | 0.805% | 2.406% | 3.013% | 0.194% | 0.084% |
| g | 2.015% | 0.866% | 3.009% | 1.768% | 1.303% | 1.171% | 1.644% | 1.253% | 2.862% | 1.731% | 3.403% | 4.077% | 4.241% | 0.392% | 0.092% |
| h | 6.094% | 0.737% | 4.577% | 0.703% | 0.781% | 0.384% | 0.636% | 1.212% | 2.090% | 1.015% | 2.380% | 1.621% | 1.871% | 1.851% | 1.356% |
| i | 6.966% | 7.529% | 6.550% | 6.247% | 6.186% | 10.012% | 10.143% | 9.600%* | 5.817% | 8.328% | 6.499% | 6.000% | 7.578% | 10.817% | 6.073% |
| j | 0.153% | 0.613% | 0.268% | 0.493% | 0.397% | 3.501% | 0.011% | 0.034% | 0.614% | 1.836% | 1.46% | 0.730% | 1.144% | 2.042% | 1.433% |
| k | 0.772% | 0.049% | 1.417% | 0.011% | 0.015% | 4.163% | 0.009% | 5.683% | 3.140% | 2.753% | 2.248% | 3.395% | 3.314% | 4.973% | 2.894% |
| l | 4.025% | 5.456% | 3.437% | 4.967% | 2.779% | 6.104% | 6.510% | 5.922% | 5.275% | 2.564% | 3.568% | 5.229% | 4.532% | 5.761% | 3.802% |
| m | 2.406% | 2.968% | 2.534% | 3.157% | 4.738% | 2.994% | 2.512% | 3.752% | 3.471% | 2.515% | 2.213% | 3.237% | 4.041% | 3.202% | 2.446% |
| n | 6.749% | 7.095% | 9.776% | 6.712% | 4.446% | 7.955% | 6.883% | 7.987% | 8.542% | 6.237% | 10.032% | 7.240% | 7.711% | 8.826% | 6.468% |
| o | 7.507% | 5.796% | 2.594% | 8.683% | 9.735% | 8.779% | 9.832% | 2.976% | 4.482% | 6.667% | 6.063% | 4.636% | 2.166% | 5.614% | 6.695% |
| p | 1.929% | 2.521% | 0.670% | 2.510% | 2.523% | 2.755% | 3.056% | 0.886% | 1.839% | 2.445% | 1.57% | 1.756% | 0.789% | 1.842% | 1.906% |
| q | 0.095% | 1.362% | 0.018% | 0.877% | 1.204% | 0 | 0.505% | 0 | 0.020% | 0 | 0.009% | 0.007% | 0 | 0.013% | 0.001% |
| r | 5.987% | 6.693% | 7.003% | 6.871% | 6.530% | 5.914% | 6.367% | 7.722% | 8.431% | 5.243% | 6.411% | 8.956% | 8.581% | 2.872% | 4.799% |
| s | 6.327% | 7.948% | 7.270% | 7.977% | 6.805% | 6.092% | 4.981% | 3.014% | 6.590% | 5.224% | 3.73% | 5.805% | 5.630% | 7.862% | 5.212% |
| t | 9.056% | 7.244% | 6.154% | 4.632% | 4.336% | 5.276% | 5.623% | 3.314% | 7.691% | 2.475% | 6.79% | 6.862% | 4.953% | 8.750% | 5.727% |
| u | 2.758% | 6.311% | 4.166% | 2.927% | 3.639% | 3.183% | 3.011% | 3.235% | 1.919% | 2.062% | 1.99% | 1.979% | 4.562% | 5.008% | 2.160% |
| v | 0.978% | 1.838% | 0.846% | 1.138% | 1.575% | 1.904% | 2.097% | 0.959% | 2.415% | 0.012% | 2.85% | 2.332% | 2.437% | 2.250% | 5.344% |
| w | 2.360% | 0.074% | 1.921% | 0.017% | 0.037% | 0 | 0.033% | 0 | 0.142% | 5.813% | 1.52% | 0.069% | 0 | 0.094% | 0.016% |
| x | 0.150% | 0.427% | 0.034% | 0.215% | 0.253% | 0 | 0.003% | 0 | 0.159% | 0.004% | 0.036% | 0.028% | 0.046% | 0.031% | 0.027% |
| y | 1.974% | 0.128% | 0.039% | 1.008% | 0.006% | 0 | 0.020% | 3.336% | 0.708% | 3.206% | 0.035% | 0.698% | 0.900% | 1.745% | 1.043% |
| z | 0.074% | 0.326% | 1.134% | 0.467% | 0.470% | 0.494% | 1.181% | 1.500% | 0.070% | 4.852% | 1.39% | 0.034% | 0 | 0.051% | 1.503% |
| à | 0 | 0.486% | 0 | 0 | 0.072% | 0 | 0.635% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| â | 0 | 0.051% | 0 | 0 | 0.562% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| á | 0 | 0 | 0 | 0.502% | 0.118% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.799% | 0 | 0.867% |
| å | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.338% | 0 | 0 | 1.190% | 0 | 0.003% | 0 |
| ä | 0 | 0 | 0.578% | 0 | 0 | 0 | 0 | 0 | 1.797% | 0 | 0 | 0 | 0 | 3.577% | 0 |
| ã | 0 | 0 | 0 | 0 | 0.733% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ą | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.699% | 0 | 0 | 0 | 0 | 0 |
| æ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.872% | 0.867% | 0 | 0 |
| œ | 0 | 0.018% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ç | 0 | 0.085% | 0 | 0 | 0.530% | 0 | 0 | 1.156% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ĉ | 0 | 0 | 0 | 0 | 0 | 0.657% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ć | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.743% | 0 | 0 | 0 | 0 | 0 |
| č | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.462% |
| ď | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.015% |
| ð | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4.393% | 0 | 0 |
| è | 0 | 0.271% | 0 | 0 | 0 | 0 | 0.263% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| é | 0 | 1.504% | 0 | 0.433% | 0.337% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.647% | 0 | 0.633% |
| ê | 0 | 0.218% | 0 | 0 | 0.450% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ë | 0 | 0.008% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ę | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.035% | 0 | 0 | 0 | 0 | 0 |
| ě | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.222% |
| ĝ | 0 | 0 | 0 | 0 | 0 | 0.691% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ğ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.125% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ĥ | 0 | 0 | 0 | 0 | 0 | 0.022% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| î | 0 | 0.045% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ì | 0 | 0 | 0 | 0 | 0 | 0 | 0.030% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| í | 0 | 0 | 0 | 0.725% | 0.132% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.570% | 0 | 1.643% |
| ï | 0 | 0.005% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ı | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.114%* | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ĵ | 0 | 0 | 0 | 0 | 0 | 0.055% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ł | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.109% | 0 | 0 | 0 | 0 | 0 |
| ñ | 0 | 0 | 0 | 0.311% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ń | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.362% | 0 | 0 | 0 | 0 | 0 |
| ň | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.007% |
| ò | 0 | 0 | 0 | 0 | 0 | 0 | 0.002% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ö | 0 | 0 | 0.443% | 0 | 0 | 0 | 0 | 0.777% | 1.305% | 0 | 0 | 0 | 0.777% | 0.444% | 0 |
| ô | 0 | 0.023% | 0 | 0 | 0.635% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ó | 0 | 0 | 0 | 0.827% | 0.296% | 0 | 0 | 0 | 0 | 1.141% | 0 | 0 | 0.994% | 0 | 0.024% |
| ø | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.939% | 0 | 0 | 0 |
| ř | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.380% |
| ŝ | 0 | 0 | 0 | 0 | 0 | 0.385% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ş | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.780% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ś | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.814% | 0 | 0 | 0 | 0 | 0 |
| š | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.688% |
| ß | 0 | 0 | 0.307% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ť | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.006% |
| þ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.455% | 0 | 0 |
| ù | 0 | 0.058% | 0 | 0 | 0 | 0 | 0.166% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ú | 0 | 0 | 0 | 0.168% | 0.207% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.613% | 0 | 0.045% |
| û | 0 | 0.060% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ŭ | 0 | 0 | 0 | 0 | 0 | 0.520% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ü | 0 | 0 | 0.995% | 0.012% | 0.026% | 0 | 0 | 1.854% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ů | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.204% |
| ý | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.228% | 0 | 0.995% |
| ź | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.078% | 0 | 0 | 0 | 0 | 0 |
| ż | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.706% | 0 | 0 | 0 | 0 | 0 |
| ž | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.721% |
*See Dotted and dotless I
The figure below illustrates the frequency distributions of the 26 most common Latin letters across some languages. All of these languages use a similar 25+ character alphabet.
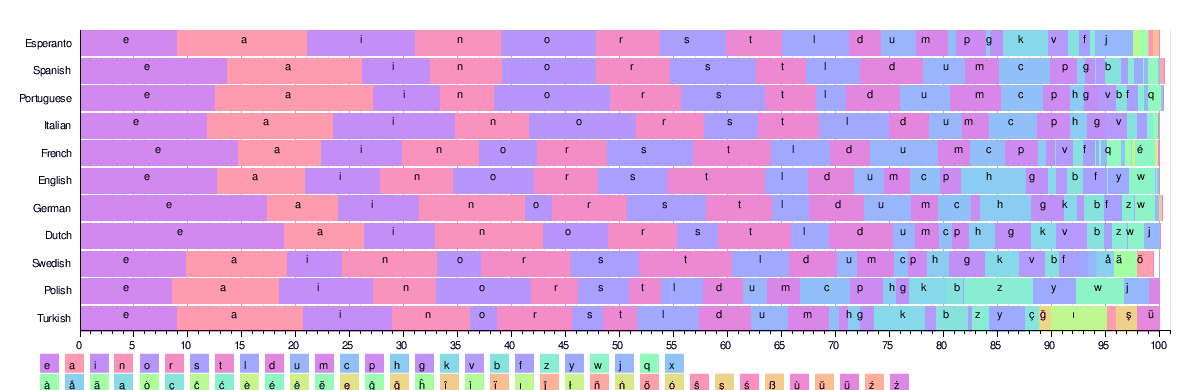
Based on these tables, the 'etaoin shrdlu'-equivalent results for each language is as follows:
- French: 'esait nruol'; (Indo-European: Romance; traditionally, 'esartinulop' is used, in part for its ease of pronunciation[33])
- Spanish: 'eaosr nidlt'; (Indo-European: Romance)
- Portuguese: 'aeosr idmnt' (Indo-European: Romance)
- Italian: 'eaion lrtsc'; (Indo-European: Romance)
- Esperanto: 'aieon lsrtk' (artificial language – influenced by Indo-European languages, Romance, Germanic mostly)
- German: 'enisr atdhu'; (Indo-European: Germanic)
- Swedish: 'eanrt sildo'; (Indo-European: Germanic)
- Turkish: 'aeinr lkdım'; (Altaic: Turkic)
- Dutch: 'enati rodsl'; (Indo-European: Germanic)[29]
- Polish: 'aieon wrszc'; (Indo-European: Slavic)
- Danish: 'ernta idslo'; (Indo-European: Germanic)
- Icelandic: 'arnie stulð'; (Indo-European: Germanic)
- Finnish: 'ainte slouk'; (Uralic: Finnic)
- Czech: 'aeoni tvsrl'; (Indo-European: Slavic)
See also
- Corpus linguistics
- ETAOIN SHRDLU
- RSTLNE (Wheel of Fortune)
- Frequency analysis (cryptanalysis)
- Linotype machine
- Most common words in English
- Scrabble
- Arabic Letter Frequency
References
- ↑ Moreno, Marsha Lynn (Spring 2005). "Frequency Analysis in Light of Language Innovation" (PDF). Math UCSD. Retrieved 19 February 2015.
- ↑ Zim, Herbert Spencer. (1961). Codes & Secret Writing: Authorized Abridgement. Scholastic Book Services. OCLC 317853773.
- ↑ http://www.oxforddictionaries.com/words/british-and-american-spelling
- ↑ Li, Wentian; Miramontes, Pedro (2011). "Fitting ranked English and Spanish letter frequency distribution in US and Mexican presidential speeches". Journal of Quantitative Linguistics. 18 (4): 359. doi:10.1080/09296174.2011.608606.
- ↑ Gusein-Zade, S.M. (1988). "Frequency distribution of letters in the Russian language". Probl. Peredachi Inf. 24 (4): 102–7.
- ↑ Gamow, George; Ycas, Martynas (1955). "Statistical correlation of protein and ribonucleic acid composition" (PDF). Proc. Natl. Acad. Sci. 41 (12): 1011–19. doi:10.1073/pnas.41.12.1011. PMC 528190
 . PMID 16589789.
. PMID 16589789. - ↑ Friedrich L. Bauer. "Decrypted Secrets: Methods and Maxims of Cryptology". 2006. p. 57.
- ↑ Greg Goebel. "The Rise Of Field Ciphers: straddling checkerboard ciphers" 2009.
- ↑ Dirk Rijmenants. "One-time Pad"
- ↑ Poe, Edgar Allan. "The works of Edgar Allan Poe in five volumes". Project Gutenberg.
- ↑ "What is the frequency of the letters of the alphabet in English?". Oxford Dictionary. Oxford University Press. Retrieved 29 December 2012.
- ↑ Mička, Pavel. "Letter frequency (English)". Algoritmy.net.
- ↑ "Frequency Table". cornell.edu.
- ↑ "Statistical Distributions of English Text". data-compression.com.
- ↑ Lee, E. Stewart. "Essays about Computer Security" (PDF). University of Cambridge Computer Laboratory. p. 181.
- ↑ Herbert Marvin Ohlman. "Subject-Word Letter Frequencies with Applications to Superimposed Coding". Proceedings of the International Conference on Scientific Information (1959).
- ↑ Singh, Simon. "The Black Chamber: Hints and Tips". Retrieved 7 March 2016.
- ↑ Hemlata Pande and H. S. Dhami. "Mathematical Modelling of Occurrence of Letters and Word’s Initials in Texts of Hindi Language".
- ↑ Calculated from "Project Gutenberg Selections" available from the NLTK Corpora
- ↑ "CorpusDeThomasTempé". Retrieved 2007-06-15.
- ↑ Beutelspacher, Albrecht (2005). Kryptologie (7 ed.). Wiesbaden: Vieweg. p. 10. ISBN 3-8348-0014-7.
- ↑ Pratt, Fletcher (1942). Secret and Urgent: the Story of Codes and Ciphers. Garden City, N.Y.: Blue Ribbon Books. pp. 254–5. OCLC 795065.
- ↑ "Frequência da ocorrência de letras no Português". Retrieved 2009-06-16.
- ↑ "La Oftecoj de la Esperantaj Literoj". Retrieved 2007-09-14.
- ↑ Singh, Simon; Galli, Stefano (1999). Codici e Segreti (in Italian). Milano: Rizzoli. ISBN 978-8-817-86213-4. OCLC 535461359.
- ↑ Sefik Ilkin Serengil, Murat Akin. "Attacking Turkish Texts Encrypted by Homophonic Cipher" Proceedings of the 10th WSEAS International Conference on Electronics, Hardware, Wireless and Optical Communications, pp.123-126, Cambridge, UK, February 20–22, 2011.
- ↑ "Practical Cryptography". Retrieved 2013-10-30.
- ↑ Wstęp do kryptologii, counting [space] 17.2%, [dot point] 0.9%, [comma] 0.9% and [semicolon] 0.5%
- 1 2 "Letterfrequenties". Genootschap OnzeTaal. Retrieved 2009-05-17.
- ↑ "Practical Cryptography". Retrieved 2013-10-24.
- ↑ "Practical Cryptography". Retrieved 2013-10-24.
- ↑ "Practical Cryptography". Retrieved 2013-10-24.
- ↑ Perec, Georges; Alphabets; Éditions Galilée, 1976
- Notes
Some useful tables for single letter, digram, trigram, tetragram, and pentagram frequencies based on 20,000 words that take into account word-length and letter-position combinations for words 3 to 7 letters in length. The references are as follows:
- Mayzner, M.S.; Tresselt, M.E. (1965). "Tables of single-letter and digram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (2): 13–32. OCLC 639975358.
- Mayzner, M.S.; Tresselt, M.E.;Wolin, B.< R.< (1965). "Tables of trigram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (3): 33–78.
- Mayzner, M.S.; Tresselt, M.E.;Woliin, B.< R,.. (1965). "Tables of tetragram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (4): 79–143.
- Mayzner, M.S.; Tresselt, M.E.Wolin, B,.< R.> (1965). "Tables of pentagram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (5): 144–190.
External links
- A site with content of Cryptographical Mathematics by Robert Edward Lewand
- Some examples of letter frequency rankings in some common languages
- JavaScript Heatmap Visualization showing letter frequencies of texts on different keyboard layouts
- An updated version of Mayzner's work using Google books Ngrams data set by Peter Norvig
