Hidden oscillation

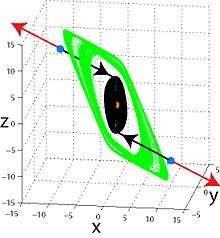
An oscillation in a dynamical system can be easily localized numerically if initial conditions from its open neighborhood lead to long-run behavior that approaches the oscillation. Such an oscillation (or set of oscillations) is called an attractor, and its attracting set is called the basin of attraction. Thus, from a computational point of view the following classification of attractors based on the simplicity of finding basin of attraction in the phase space is suggested:[1][2][3] an attractor is called a hidden attractor if its basin of attraction does not intersect with small neighborhoods of equilibria, otherwise it is called a self-excited attractor.
Self-excited attractor localization
Self-excited attractors can be localized numerically by the standard computational procedure, in which after a transient process a trajectory, started from a point of unstable manifold in a neighborhood of equilibrium, reaches a state of oscillation therefore one can easily identify it. Here It is essential to consider numerical localization procedures in forward and backward time, since computation in backward time may localize also an unstable oscillation.
Classical attractors in the well-known dynamical systems of Van der Pol, Beluosov–Zhabotinsky, Lorenz, Rössler, Chua and many others are self-excited attractors and can be obtained numerically, with relative ease, by standard computational procedures described above.
Hidden attractor localization
For numerical localization of hidden attractors it is necessary to develop special analytical-numerical procedures, since there are no similar transient processes leading to such attractors from neighborhoods of equilibria. For example, hidden attractor is periodic or chaotic attractor in the system without equilibria or with the only stable equilibrium (a special case of multistability and coexistence of attractors).
One of the simplest examples of hidden oscillations is internal nested limit cycles in two-dimensional systems. Other examples of hidden oscillations are counterexamples to Aizerman's and Kalman's conjectures on absolute stability in automatic control theory (where unique stable equilibrium points and attracting periodic solutions coexist), which can be constructed for system dimensions not less than three and four respectively.
In 2010, for the first time, a chaotic hidden attractor was discovered [1] [2] in Chua's circuit, which is described by a three-dimensional dynamical system.
While for two-dimensional systems hidden oscillations can be investigated using analytical methods (see, e.g., results on the second part of Hilbert's 16th problem), for the study of stability and oscillations in complex nonlinear multidimensional systems numerical methods are often used. In the multi-dimensional case the integration of trajectories with random initial data is unlikely to provide localization of a hidden attractor, since a basin of attraction may be very small and the attractor dimension itself may be much less than the dimension of the considered system. Therefore, for numerical localization of hidden attractors in multi-dimensional space it is necessary to develop special analytical-numerical computational procedures, [4] [5] [6] [7] [8][9] which allow one to choose initial data in the attraction domain of the hidden oscillation (which does not contain neighborhoods of equilibria) and then to perform trajectory computation there. Here it is turned out to be effective the methods based on homotopy and numerical continuation: a sequence of similar systems is constructed, such that for the first (starting) system the initial data for numerical computation of oscillating solution (starting oscillation) can be obtained analytically, and then the transformation of this starting oscillation in the transition from one system to another is followed numerically.
References
- 1 2 Kuznetsov N.V.; Leonov G.A.; Vagaitsev V.I. (2010). "Analytical-numerical method for attractor localization of generalized Chua's system". IFAC Proceedings Volumes (IFAC-PapersOnline). 4 (1): 29–33. doi:10.3182/20100826-3-TR-4016.00009.
- 1 2 Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors" (PDF). Physics Letters. 375 (23): 2230–2233. doi:10.1016/j.physleta.2011.04.037.
- ↑ Leonov G.A.; Kuznetsov N.V. (2013). "Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits". International Journal of Bifurcation and Chaos. 23 (1): art. no. 1330002. doi:10.1142/S0218127413300024.
- ↑ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2010). "Algorithm for localizing Chua attractors based on the harmonic linearization method" (PDF). Doklady Mathematics. 82 (1): 663–666. doi:10.1134/S1064562410040411.
- ↑ Leonov G.A.; Kuznetsov N.V. (2011). "Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems" (PDF). Doklady Mathematics. 84 (1): 475–481. doi:10.1134/S1064562411040120.
- ↑ Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. (2011). "Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits" (PDF). Journal of Computer and Systems Sciences International. 50 (5): 511–543. doi:10.1134/S106423071104006X.
- ↑ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2012). "Hidden attractor in smooth Chua systems" (PDF). Physica D. 241 (18): 1482–1486. doi:10.1016/j.physd.2012.05.016.
- ↑ Kuznetsov N.; Kuznetsova O.; Leonov G.; Vagaitsev V. (2013). "Analytical-numerical localization of hidden attractor in electrical Chua's circuit" (PDF). Lecture Notes in Electrical Engineering (Springer). 174 LNEE: 149–158. doi:10.1007/978-3-642-31353-0_11.