Induction equation

Induction equation, as one of the magnetohydrodynamic equations, is a partial differential equation with spatial and time variables that relates the magnetic and velocity fields of an electrically conductive fluid such as a plasma. This equation can be derived using the Maxwell's equations along with the so-called Ohm's law. Induction equation has also a major role in plasma physics and astrophysics specially in the magnetic dynamo theory.

Mathematical statement

Maxwell's equations describing the Faraday's and Ampere's laws read

$\vec{\nabla}\times\vec{E}=-{\partial \vec{B} \over \partial t},$

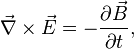
and

$\vec{\nabla}\times\vec{B}=\mu_0\vec{J},$

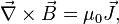
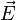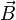where the displacement current has been neglected as it usually has small effects in astrophysical applications as well as in most of laboratory plasmas. Here, $\vec{E}$, and $\vec{B}$ are, respectively, electric and magnetic fields, and 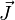$\vec{J}$ is the electric current. 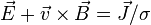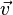The electric field can be related to the current density using the Ohm's law, $\vec{E}+\vec{v}\times\vec{B}=\vec{J}/\sigma$ where $\vec{v}$ is the velocity field, and 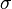$\sigma$ is the electric conductivity of the fluid. Taking the time derivative of the first equation, and combining the result with the second one, yield

${\partial \vec{B} \over \partial t}=\eta \nabla^2 \vec{B}+\vec{\nabla}\times(\vec{v}\times\vec{B}),$

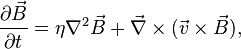
where 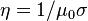$\eta=1/\mu_0\sigma$ is the magnetic diffusivity. (In the literature, the electrical resistivity, defined as 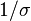$1/\sigma$, is also sometimes called magnetic diffusivity, defined as 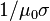$1/\mu_0\sigma$, while they have different values in SI units.) The above equation is the induction equation for an electrically resistive fluid.

If the fluid moves with a typical speed 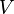$V$ and a typical length scale 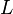$L$, then

$\eta \nabla^2 \vec{B} \sim {\eta B \over L^2}, \vec{\nabla}\times (\vec{v}\times \vec{B}) \sim {VB\over L}.$

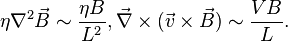
The ratio of these quantities, which is a dimensionless parameter, is called the magnetic Reynolds number:

$R_m={LV\over\eta}$.

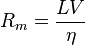Perfectly conducting limit

For a fluid with infinite electric conductivity, 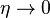$\eta \rightarrow 0$, the first term in the induction equation vanishes. This is equivalent to a very large magnetic Reynolds number. For example, it can be of order 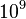$10^9$ in a typical star. In this case, the fluid can be called a perfect or ideal fluid. So, the induction equation for an ideal conductive fluid such as most astrophysical plasmas is

${\partial \vec{B} \over \partial t}=\vec{\nabla}\times(\vec{v}\times\vec{B}).$

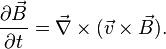
This is taken to be a good approximation in dynamo theory, used to explain the magnetic field evolution in the astrophysical environments such as stars, galaxies and accretion discs.

Diffusive limit

For very small magnetic Reynolds numbers, the diffusive term overcomes the convective term. For example, in an electrically resistive fluid with large values of 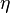$\eta$, the magnetic field is diffused away very fast, and the Alfvén's Theorem cannot be applied. This means magnetic energy is dissipated to heat and other types of energy. The induction equation then reads

${\partial \vec{B} \over \partial t}=\eta \nabla^2 \vec{B}.$

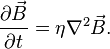
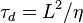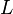It is common to define a dissipation time scale $\tau_d=L^2/\eta$ which is the time scale for the dissipation of magnetic energy over a length scale $L$.

See also

• Alfvén's Theorem
• Magnetohydrodynamics
• Maxwell's equations