Jim Stasheff

James Dillon "Jim" Stasheff (born January 15, 1936 in New York)[1][2] is an American mathematician, a professor emeritus of mathematics at the University of North Carolina at Chapel Hill.[3] He works in algebraic topology and algebra as well as their applications to physics.
Biography
Stasheff did his undergraduate studies in mathematics at the University of Michigan, graduating in 1956.[1] Stasheff then began his graduate studies at Princeton University; his notes for a 1957 course by John Milnor on characteristic classes first appeared in mimeographed form and later in 1974 in revised form book with Stasheff as a co-author.[4] After his second year at Princeton, he moved to Oxford University on a Marshall Scholarship. Two years later in 1961, with a pregnant wife, needing an Oxford degree to get reimbursed for his return trip to the US, and yet still feeling attached to Princeton, he split his thesis into two parts (one topological, the other algebraic) and earned two doctorates, a D.Phil. from Oxford under the supervision of Ioan James and a Ph.D. later the same year from Princeton under the supervision of John Coleman Moore.[1][5][6]
From 1961 to 1962, Stasheff was a C.L.E. Moore instructor at the Massachusetts Institute of Technology. Then in 1962 joined the faculty of University of Notre Dame as an assistant professor; he was promoted to full professor there in 1968. He visited Princeton University from 1968 to 1969 and then stayed there the next year as a Sloan Fellow. Then in 1970 he moved to Temple University, where he held a position until 1978. In 1976, he joined the UNC faculty.[1] He has also visited the Institute for Advanced Study, Lehigh University, Rutgers University, and the University of Pennsylvania.
Stasheff was an editor of the Transactions of the American Mathematical Society. He has been married since 1959 and has two children.
Research
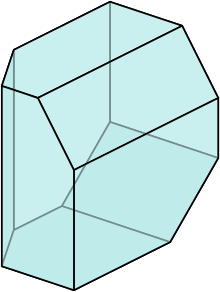
Stasheff's research contributions include the study of associativity in loop spaces and the construction of the associahedron (also called the Stasheff polytope), ideas leading to the theory of operads; homotopy theoretic approaches to Hilbert's fifth problem on the characterization of Lie groups; and the study of Poisson algebras in mathematical physics.[1]
In the 1960s he wrote fundamental papers on higher homotopy theory and homotopy algebras. He introduced , Stasheff algebras and Stasheff polytopes.
In the 1980s he turned to the application of characteristic classes and other topological and algebraic concepts in mathematical physics, first in the algebraic structure of anomalies in quantum field theory, where he worked with among others, Tom Kephart and Paolo Cotta-Ramusino. He referred to the research field as cohomological physics.
Awards and honors
In 2012 he became a fellow of the American Mathematical Society.[7]
Selected publications
- Milnor, John W.; Stasheff, James D. (1974), Characteristic Classes, Annals of Mathematics Studies, 76, Princeton, NJ: Princeton University Press, ISBN 0-691-08122-0.
- Stasheff, James Dillon (1963), "Homotopy associativity of H-spaces. I, II", Transactions of the American Mathematical Society, 108: 275–292, 293–312, doi:10.2307/1993609, MR 0158400.
References
- 1 2 3 4 5 McCleary, John (1999), "An appreciation of the work of Jim Stasheff", in McCleary, John, Higher Homotopy Structures in Topology and Mathematical Physics: Proceedings of an International Conference, June 13–15, 1996 at Vassar College, Poughkeepsie, New York, to Honor the Sixtieth Birthday of Jim Stasheff (PDF), Contemporary Mathematics, 227, American Mathematical Society, pp. 1–16, ISBN 9780821809136.
- ↑ American Men and Women of Science, Thomson Gale 2004
- ↑ Emeritus faculty, UNC Chapel Hill Mathematics, retrieved 2012-03-24.
- ↑ Milnor & Stasheff 1974.
- ↑ James Dillon Stasheff at the Mathematics Genealogy Project
- ↑ Stasheff, J. (2000), Reminiscences of a graduate student in Princeton in the late 1950s (PDF), Temple–Villanova History of Math Seminar, retrieved 2012-04-12
- ↑ List of Fellows of the American Mathematical Society, retrieved 2013-08-05.