Classification of discontinuities
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. This article describes the classification of discontinuities in the simplest case of functions of a single real variable taking real values.
The oscillation of a function at a point quantifies these discontinuities as follows:
- in a removable discontinuity, the distance that the value of the function is off by is the oscillation;
- in a jump discontinuity, the size of the jump is the oscillation (assuming that the value at the point lies between these limits from the two sides);
- in an essential discontinuity, oscillation measures the failure of a limit to exist.
Classification
For each of the following, consider a real valued function f of a real variable x, defined in a neighborhood of the point x0 at which f is discontinuous.
Removable discontinuity

Consider the function
The point x0 = 1 is a removable discontinuity. For this kind of discontinuity:
The one-sided limit from the negative direction:
and the one-sided limit from the positive direction:
at x0 both exist, are finite, and are equal to L = L− = L+. In other words, since the two one-sided limits exist and are equal, the limit L of f(x) as x approaches x0 exists and is equal to this same value. If the actual value of f(x0) is not equal to L, then x0 is called a removable discontinuity. This discontinuity can be 'removed to make f continuous at x0', or more precisely, the function
is continuous at x = x0.
It is important to realize that the term removable discontinuity is sometimes used by abuse of terminology for cases in which the limits in both directions exist and are equal, while the function is undefined at the point x0.[1] This use is abusive because continuity and discontinuity of a function are concepts defined only for points in the function's domain. Such a point not in the domain is properly named a removable singularity.
Jump discontinuity
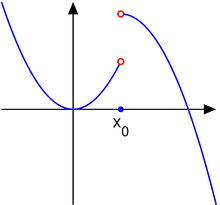
Consider the function
Then, the point x0 = 1 is a jump discontinuity.
In this case, a single limit does not exist because the one-sided limits, L− and L+, exist and are finite, but are not equal: since, L− ≠ L+, the limit L does not exist. Then, x0 is called a jump discontinuity, step discontinuity, or discontinuity of the first kind. For this type of discontinuity, the function f may have any value at x0.
Essential discontinuity
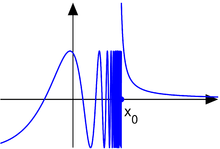
For an essential discontinuity, only one of the two one-sided limits needs not to exist or is infinite. Consider the function
Then, the point is an essential discontinuity.
In this case, one or both of the limits and does not exist or is infinite so x0 is an essential discontinuity, infinite discontinuity, or discontinuity of the second kind. (This is distinct from the term essential singularity which is often used when studying functions of complex variables.)
The set of discontinuities of a function
The set of points at which a function is continuous is always a Gδ set. The set of discontinuities is an Fσ set.
The set of discontinuities of a monotonic function is at most countable. This is Froda's theorem.
Thomae's function is discontinuous at every rational point, but continuous at every irrational point.
The indicator function of the rationals, also known as the Dirichlet function, is discontinuous everywhere.
See also
Notes
- ↑ See, for example, the last sentence in the definition given at Mathwords.
References
- Malik, S.C.; Arora, Savita (1992). Mathematical Analysis (2nd ed.). New York: Wiley. ISBN 0-470-21858-4..
External links
- "Discontinuous". PlanetMath.
- "Discontinuity" by Ed Pegg, Jr., The Wolfram Demonstrations Project, 2007.
- Weisstein, Eric W. "Discontinuity". MathWorld.
- Kudryavtsev, L.D. (2001), "Discontinuity point", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4