List of graphs

This partial list of graphs contains definitions of graphs and graph families which are known by particular names, but do not have a Wikipedia article of their own.

For collected definitions of graph theory terms that do not refer to individual graph types, such as vertex and path, see Glossary of graph theory. For links to existing articles about particular kinds of graphs, see Category:Graphs.

Gear

G4

A gear graph, denoted Gn is a graph obtained by inserting an extra vertex between each pair of adjacent vertices on the perimeter of a wheel graph Wn. Thus, Gn has 2n+1 vertices and 3n edges.[1] Gear graphs are examples of squaregraphs, and play a key role in the forbidden graph characterization of squaregraphs.[2] Gear graphs are also known as cogwheels and bipartite wheels.

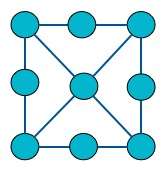
Grid

A grid graph is a unit distance graph corresponding to the square lattice, so that it is isomorphic to the graph having a vertex corresponding to every pair of integers (a, b), and an edge connecting (a, b) to (a+1, b) and (a, b+1). The finite grid graph Gm,n is an m×n rectangular graph isomorphic to the one obtained by restricting the ordered pairs to the range 0 ≤ a < m, 0 ≤ b < n. Grid graphs can be obtained as the Cartesian product of two paths: Gm,n = Pm × Pn. Every grid graph is a median graph.[3]

Helm

A helm graph, denoted Hn is a graph obtained by attaching a single edge and node to each node of the outer circuit of a wheel graph Wn.[4][5]

Lobster

A lobster graph is a tree in which all the vertices are within distance 2 of a central path.[6][7] Compare caterpillar.

Web

The web graph W4,2 is a cube.

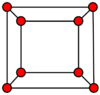
The web graph Wn,r is a graph consisting of r concentric copies of the cycle graph Cn, with corresponding vertices connected by "spokes". Thus Wn,1 is the same graph as Cn, and Wn,2 is a prism.

A web graph has also been defined as a prism graph Yn+1, 3, with the edges of the outer cycle removed.[5][8]

See also

Gallery of named graphs

References

  1. ↑ Weisstein, Eric W. "Gear graph". MathWorld.
  2. ↑ Bandelt, H.-J.; Chepoi, V.; Eppstein, D. (2010), "Combinatorics and geometry of finite and infinite squaregraphs", SIAM Journal on Discrete Mathematics, 24 (4): 1399–1440, arXiv:0905.4537Freely accessible, doi:10.1137/090760301
  3. ↑ Weisstein, Eric W. "Grid graph". MathWorld.
  4. ↑ Weisstein, Eric W. "Helm graph". MathWorld.
  5. 1 2 http://www.combinatorics.org/Surveys/ds6.pdf
  6. ↑ "Google Discussiegroepen". Groups.google.com. Retrieved 2014-02-05.
  7. ↑ Weisstein, Eric W. "Lobster". MathWorld.
  8. ↑ Weisstein, Eric W. "Web graph". MathWorld.
This article is issued from Wikipedia - version of the 10/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.