Prism (geometry)
| Set of uniform prisms | |
|---|---|
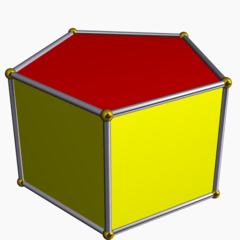
 (A hexagonal prism is shown) | |
| Type | uniform polyhedron |
| Conway polyhedron notation | Pn |
| Faces | 2+n total: 2 {n} n {4} |
| Edges | 3n |
| Vertices | 2n |
| Schläfli symbol | {n}×{} or t{2, n} |
| Coxeter diagram | |
| Vertex configuration | 4.4.n |
| Symmetry group | Dnh, [n,2], (*n22), order 4n |
| Rotation group | Dn, [n,2]+, (n22), order 2n |
| Dual polyhedron | bipyramids |
| Properties | convex, semi-regular vertex-transitive |
 n-gonal prism net (n = 9 here) | |
In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.
General, right and uniform prisms
A right prism is a prism in which the joining edges and faces are perpendicular to the base faces.[1] This applies if the joining faces are rectangular. If the joining edges and faces are not perpendicular to the base faces, it is called an oblique prism.
For example a parallelepiped is an oblique prism of which the base is a parallelogram, or equivalently a polyhedron with six faces which are all parallelograms.
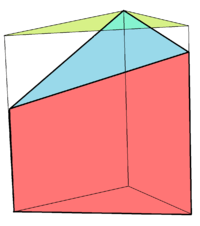
A truncated prism is a prism with nonparallel top and bottom faces.[2]
Some texts may apply the term rectangular prism or square prism to both a right rectangular-sided prism and a right square-sided prism. A right p-gonal prism with rectangular sides has a Schläfli symbol { } × {p}.
A right rectangular prism is also called a cuboid, or informally a rectangular box. A right square prism is simply a square box, and may also be called a square cuboid. A right rectangular prism has Schläfli symbol { }×{ }×{ }.
An n-prism, having regular polygon ends and rectangular sides, approaches a cylindrical solid as n approaches infinity.
The term uniform prism or semiregular prism can be used for a right prism with square sides, since such prisms are in the set of uniform polyhedra. A uniform p-gonal prism has a Schläfli symbol t{2,p}. Right prisms with regular bases and equal edge lengths form one of the two infinite series of semiregular polyhedra, the other series being the antiprisms.
The dual of a right prism is a bipyramid.
Volume
The volume of a prism is the product of the area of the base and the distance between the two base faces, or the height (in the case of a non-right prism, note that this means the perpendicular distance).
The volume is therefore:
where B is the base area and h is the height. The volume of a prism whose base is a regular n-sided polygon with side length s is therefore:
Surface area
The surface area of a right prism is 2 · B + P · h, where B is the area of the base, h the height, and P the base perimeter.
The surface area of a right prism whose base is a regular n-sided polygon with side length s and height h is therefore:
Schlegel diagrams
 P3 |
 P4 |
 P5 |
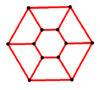 P6 |
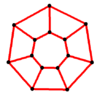 P7 |
 P8 |
Symmetry
The symmetry group of a right n-sided prism with regular base is Dnh of order 4n, except in the case of a cube, which has the larger symmetry group Oh of order 48, which has three versions of D4h as subgroups. The rotation group is Dn of order 2n, except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D4 as subgroups.
The symmetry group Dnh contains inversion iff n is even.
Prismatic polytope
A prismatic polytope is a higher-dimensional generalization of a prism. An n-dimensional prismatic polytope is constructed from two (n − 1)-dimensional polytopes, translated into the next dimension.
The prismatic n-polytope elements are doubled from the (n − 1)-polytope elements and then creating new elements from the next lower element.
Take an n-polytope with fi i-face elements (i = 0, ..., n). Its (n + 1)-polytope prism will have 2fi + fi−1 i-face elements. (With f−1 = 0, fn = 1.)
By dimension:
- Take a polygon with n vertices, n edges. Its prism has 2n vertices, 3n edges, and 2 + n faces.
- Take a polyhedron with v vertices, e edges, and f faces. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2 + f cells.
- Take a polychoron with v vertices, e edges, f faces and c cells. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2c + f cells, and 2 + c hypercells.
Uniform prismatic polytope
A regular n-polytope represented by Schläfli symbol {p, q, ..., t} can form a uniform prismatic (n + 1)-polytope represented by a Cartesian product of two Schläfli symbols: {p, q, ..., t}×{}.
By dimension:
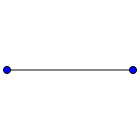
- A 0-polytopic prism is a line segment, represented by an empty Schläfli symbol {}.
- A 1-polytopic prism is a rectangle, made from 2 translated line segments. It is represented as the product Schläfli symbol {}×{}. If it is square, symmetry can be reduced: {}×{} = {4}.
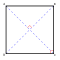 Example: Square, {}×{}, two parallel line segments, connected by two line segment sides.
Example: Square, {}×{}, two parallel line segments, connected by two line segment sides.
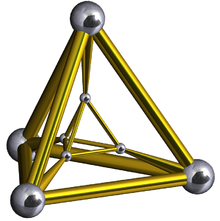
- A polygonal prism is a 3-dimensional prism made from two translated polygons connected by rectangles. A regular polygon {p} can construct a uniform n-gonal prism represented by the product {p}×{}. If p = 4, with square sides symmetry it becomes a cube: {4}×{} = {4, 3}.
 Example: Pentagonal prism, {5}×{}, two parallel pentagons connected by 5 rectangular sides.
Example: Pentagonal prism, {5}×{}, two parallel pentagons connected by 5 rectangular sides.
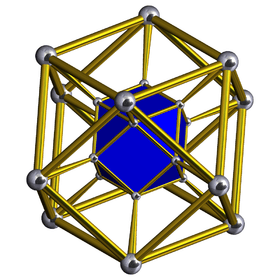
- A polyhedral prism is a 4-dimensional prism made from two translated polyhedra connected by 3-dimensional prism cells. A regular polyhedron {p, q} can construct the uniform polychoric prism, represented by the product {p, q}×{}. If the polyhedron is a cube, and the sides are cubes, it becomes a tesseract: {4, 3}×{} = {4, 3, 3}.
 Example: Dodecahedral prism, {5, 3}×{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
Example: Dodecahedral prism, {5, 3}×{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
- ...
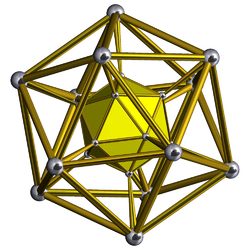
Higher order prismatic polytopes also exist as cartesian products of any two polytopes. The dimension of a polytope is the product of the dimensions of the elements. The first example of these exist in 4-dimensional space are called duoprisms as the product of two polygons. Regular duoprisms are represented as {p}×{q}.
| Polyhedron | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coxeter | ||||||||||
| Tiling | ||||||||||
| Config. | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 |
Twisted prism
A twisted prism is a nonconvex prism polyhedron constructed by a uniform q-prism with the side faces bisected on the square diagonal, and twisting the top, usually by 180/q degrees in the same direction, causing side triangles to be concave.[3][4]
A twisted prism cannot be triangulated into tetrahedra without adding new vertices. The smallest case, triangular form, is called a Schönhardt polyhedron.
A twisted prism is topologically identical to the antiprism, but has half the symmetry: Dn, [n,2]+, order 2n. It can be seen as a convex antiprism, with tetrahedra removed between pairs of triangles.
| 3-gonal | 4-gonal | 12-gonal | |
|---|---|---|---|
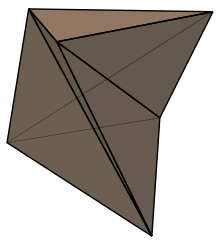 Schönhardt polyhedron |
 Twisted square prism |
 Square antiprism |
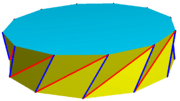 Twisted dodecagonal antiprism |
.
Related polyhedra and tilings
| Polyhedron | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coxeter | ||||||||||
| Tiling | ||||||||||
| Config. | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 |
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Name | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} |
| Cupola |  Digonal cupola |
 Triangular cupola |
 Square cupola |
 Pentagonal cupola |
 Hexagonal cupola (Flat) |
| Related uniform polyhedra |
Triangular prism |
Cubocta- hedron |
Rhombi- cubocta- hedron |
Rhomb- icosidodeca- hedron |
Rhombi- trihexagonal tiling |
Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.
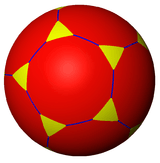
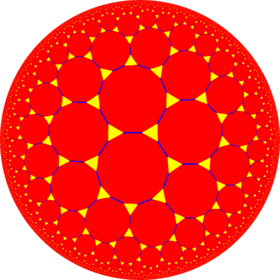
| *n32 symmetry mutation of truncated tilings: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Truncated figures |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | t{12i,3} | t{9i,3} | t{6i,3} |
| Triakis figures |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of expanded tilings: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paracomp. | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure |  |
 |
 |
 |
 |
 |
 | |
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Compounds
There are 4 uniform compounds of triangular prisms:
- Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.
Honeycombs
There are 9 uniform honeycombs that include triangular prism cells:
- Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb
Related polytopes
The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −121.
| k21 figures in n dimensional | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 192 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph | 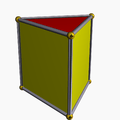 |
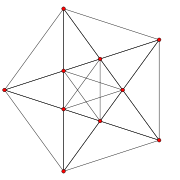 |
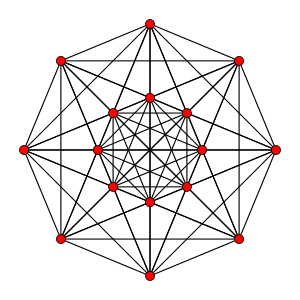 |
 |
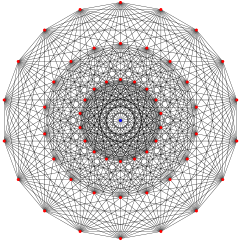 |
 |
- | - | |||
| Name | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
Four dimensional space
The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:
See also
References
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisma and antiprisms
External links
- Olshevsky, George. "Prismatic polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Nonconvex Prisms and Antiprisms
- Surface Area MATHguide
- Volume MATHguide
- Paper models of prisms and antiprisms Free nets of prisms and antiprisms
- Paper models of prisms and antiprisms Using nets generated by Stella.
- Stella: Polyhedron Navigator: Software used to create the 3D and 4D images on this page.