Multiscroll attractor

Double-scroll attractor from a simulation

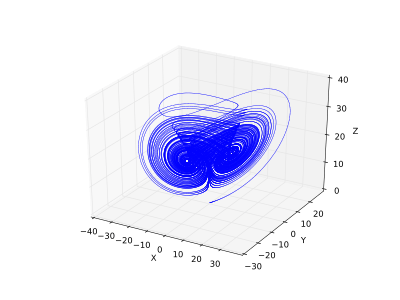
In the mathematics of dynamical systems, the double-scroll attractor (sometimes known as Chua's attractor) is a strange attractor observed from a physical electronic chaotic circuit (generally, Chua's circuit) with a single nonlinear resistor (see Chua's Diode). The double-scroll system is often described by a system of three nonlinear ordinary differential equations and a 3-segment piecewise-linear equation (see Chua's equations). This makes the system easily simulated numerically and easily manifested physically due to Chua's circuits' simple design.

Using a Chua's circuit, this shape is viewed on an oscilloscope using the X, Y, and Z output signals of the circuit. This chaotic attractor is known as the double scroll because of its shape in three-dimensional space, which is similar to two saturn-like rings connected by swirling lines.

The attractor was first observed in simulations, then realized physically after Leon Chua invented the autonomous chaotic circuit which became known as Chua's circuit.^[1] The double-scroll attractor from the Chua circuit was rigorously proven to be chaotic^[2] through a number of Poincaré return maps of the attractor explicitly derived by way of compositions of the eigenvectors of the 3-dimensional state space.^[3]

Numerical analysis of the double-scroll attractor has shown that its geometrical structure is made up of an infinite number of fractal-like layers. Each cross section appears to be a fractal at all scales.^[4] Recently, there has also been reported the discovery of hidden attractors within the double scroll.^[5]

In 1999 Guanrong Chen (陈关荣) and Ueta proprosed another double scroll chaotic attractor.^[6]

Chen system:

${\frac {dx(t)}{dt}}=a*(y(t)-x(t))$

${\frac {dy(t)}{dt}}=(c-a)*x(t)-x(t)*z(t)+c*y(t)$

${\frac {dz(t)}{dt}}=x(t)*y(t)-b*z(t)$

Plots of Chen attractor can be obtained with Runge-Kutta method：^[7]

parameters:a = 40, c = 28, b = 3

initial conditions:x(0) = -0.1, y(0) = 0.5, z(0) = -0.6

Multiscroll attractors

Multiscroll attractors also called n-scroll attractor include the Lu Chen attractor,the modified Chen chaotic attractor, PWL Duffing attractor, Rabinovich Fabrikant attractor,modified Chua chaotic attractor, that is, multiple scrolls in a single attractor.^[8]

Lu Chen attractor

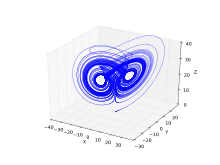
An extended Chen system with muliscroll was proposed by Jinhu Lu(吕金虎）and Guanrong Chen^[9]

Lu Chen system equation ${\frac {dx(t)}{dt}}=a*(y(t)-x(t))$

${\frac {dy(t)}{dt}}=x(t)-x(t)*z(t)+c*y(t)+u$

${\frac {dz(t)}{dt}}=x(t)*y(t)-b*z(t)$

parameters：a = 36, c = 20, b = 3, u = -15..15

initial conditions：x(0) = .1, y(0) = .3, z(0) = -.6

Modified Lu Chen attractor

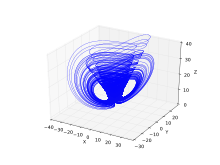
System equations:.^[9]

${\frac {dx(t)}{dt}}=a*(y(t)-x(t)),$

${\frac {dy(t)}{dt}}=(c-a)*x(t)-x(t)*f+c*y(t),$

${\frac {dz(t)}{dt}}=x(t)*y(t)-b*z(t)$

In which

$f=d0*z(t)+d1*z(t-\tau )-d2*\sin(z(t-\tau ))$

params := a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2

initv := x(0) = 1, y(0) = 1, z(0) = 14

Modified Chua chaotic attractor

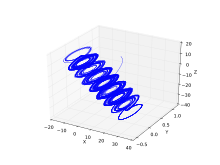
In 2001, Tang et al. proposed a modified Chua chaotic system^[10]

${\frac {dx(t)}{dt}}=\alpha *(y(t)-h)$

${\frac {dy(t)}{dt}}=x(t)-y(t)+z(t)$

${\frac {dz(t)}{dt}}=-\beta *y(t)$

In which

$h:=-b*sin({\frac {\pi *x(t)}{2*a}}+d)$

params := alpha = 10.82, beta = 14.286, a = 1.3, b = .11, c = 7, d = 0

initv := x(0) = 1, y(0) = 1, z(0) = 0

PWL Duffing chaotic attractor

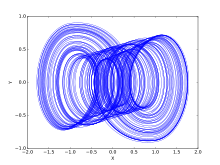
Aziz Alaoui investigated PWL Duffing equation in 2000：^[11]。

PWL Duffing system:

${\frac {dx(t)}{dt}}=y(t)$

${\frac {dy(t)}{dt}}=-m1*x(t)-(1/2*(m0-m1))*(|x(t)+1|-|x(t)-1|)-e*y(t)+\gamma *cos(\omega *t)$

params := e = .25, gamma = .14+(1/20)*i, m0 = -0.845e-1, m1 = .66, omega = 1; c := (.14+(1/20)*i)，i=-25..25;

initv := x(0) = 0, y(0) = 0；

Modified Lorenz chaotic system

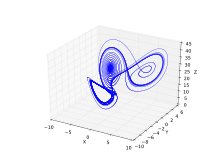
Miranda & Stone proposed a modified Lorenz system：^[12]

${\frac {dx(t)}{dt}}=1/3*(-(a+1)*x(t)+a-c+z(t)*y(t))+((1-a)*(x(t)^{2}-y(t)^{2})+(2*(a+c-z(t)))*x(t)*y(t))$$*{\frac {1}{3*{\sqrt {x(t)^{2}+y(t)^{2}}}}}$

${\frac {dy(t)}{dt}}=1/3*((c-a-z(t))*x(t)-(a+1)*y(t))+((2*(a-1))*x(t)*y(t)+(a+c-z(t))*(x(t)^{2}-y(t)^{2}))$$*{\frac {1}{3*{\sqrt {x(t)^{2}+y(t)^{2}}}}}$

${\frac {dz(t}{dt}}=1/2*(3*x(t)^{2}*y(t)-y(t)^{3})-b*z(t)$

parameters： a = 10, b = 8/3, c = 137/5；

initial conditions： x(0) = -8, y(0) = 4, z(0) = 10

See also

• The double-scroll attractor and Chua's circuit

References

1. Matsumoto, Takashi (December 1984). "A Chaotic Attractor from Chua's Circuit" (PDF). IEEE Transactions on Circuits and Systems. IEEE. CAS-31 (12): 1055–1058.
2. Chua, Leon; Motomasa Komoru; Takashi Matsumoto (November 1986). "The Double-Scroll Family" (PDF). IEEE Transactions Circuits and Systems. CAS-33 (11).
3. Chua, Leon (2007). "Chua circuits". Scholarpedia. doi:10.4249/scholarpedia.1488.
4. Chua, Leon (2007). "Fractal Geometry of the Double-Scroll Attractor". Scholarpedia. doi:10.4249/scholarpedia.1488.
5. Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors" (PDF). Physics Letters A. 375 (23): 2230–2233. doi:10.1016/j.physleta.2011.04.037.
6. Chen G., Ueta T. Yet another chaotic attractor. Journal of Bifurcation and Chaos, 1999 9:1465.
7. 阎振亚著 《复杂非线性波的构造性理论及其应用》第17页 SCIENCEP 2007年
8. Chen, Guanrong; Jinhu Lu (2006). "GENERATING MULTISCROLL CHAOTIC ATTRACTORS: THEORIES, METHODS AND APPLICATIONS" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 775–858. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
9. Jinhu Lu
10. Chen, Guanrong; Jinhu Lu (2006). "GENERATING MULTISCROLL CHAOTIC ATTRACTORS: THEORIES, METHODS AND APPLICATIONS" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 793–794. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
11. J.Lu et al p837
12. J.Liu and G Chen p834