Non-perturbative

In mathematics and physics, a non-perturbative function or process is one that cannot be accurately described by perturbation theory. An example is the function

${\displaystyle f(x)=e^{-1/x^{2}}}$.

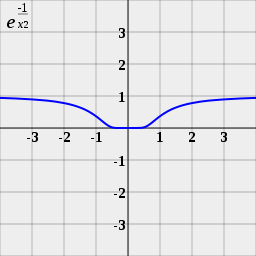
The Taylor series at x = 0 for this function is exactly zero to all orders in perturbation theory, but the function is non-zero if x ≠ 0.

The implication of this for physics is that there are some phenomena which are impossible to understand by perturbation theory, regardless of how many orders of perturbation theory we use. Instantons are an example.

Therefore, in theoretical physics, a non-perturbative solution or theory is one that does not require perturbation theory to explicate, or does not simply describe the dynamics of perturbations around some fixed background. For this reason, non-perturbative solutions and theories yield insights into areas and subjects perturbative methods cannot reveal.

See also

• Lattice QCD
• Taylor series
• Nonperturbative vacuum
• Soliton
• Sphaleron
• Instanton
• BCFW recursion
• Conformal bootstrap
• Loop quantum gravity
• Causal dynamical triangulation