Numerical sign problem

The numerical sign problem in applied mathematics refers to the difficulty of numerically evaluating the integral of a highly oscillatory function of a large number of variables. Numerical methods fail because of the near-cancellation of the positive and negative contributions to the integral. Each has to be integrated to very high precision in order for their difference to be obtained with useful accuracy.

The sign problem is one of the major unsolved problems in the physics of many-particle systems. It often arises in calculations of the properties of a quantum mechanical system with large number of strongly interacting fermions, or in field theories involving a non-zero density of strongly interacting fermions.

The sign problem in physics

In physics the sign problem is typically (but not exclusively) encountered in calculations of the properties of a quantum mechanical system with large number of strongly interacting fermions, or in field theories involving a non-zero density of strongly interacting fermions. Because the particles are strongly interacting, perturbation theory is inapplicable, and one is forced to use brute-force numerical methods. Because the particles are fermions, their wavefunction changes sign when any two fermions are interchanged (due to the symmetry of the wave function, see Pauli principle). So unless there are cancellations arising from some symmetry of the system, the quantum-mechanical sum over all multi-particle states involves an integral over a function that is highly oscillatory, and hence hard to evaluate numerically, particularly in high dimension. Since the dimension of the integral is given by the number of particles, the sign problem becomes severe in the thermodynamic limit. The field-theoretic manifestation of the sign problem is discussed below.

The sign problem is one of the major unsolved problems in the physics of many-particle systems, impeding progress in many areas:

• Condensed matter physics. It prevents the numerical solution of systems with a high density of strongly correlated electrons, such as the Hubbard model.^[1]
• Nuclear physics. It prevents the ab-initio calculation of properties of nuclear matter and hence limits our understanding of nuclei and neutron stars.
• Particle physics. It prevents the use of Lattice QCD to predict the phases and properties of quark matter.^[2]

The sign problem in field theory^[3][4]

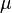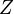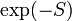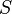In a field theory approach to multi-particle systems, the fermion density is controlled by the value of the fermion chemical potential $\mu$. One evaluates the partition function $Z$ by summing over all classical field configurations, weighted by $\exp(-S)$ where $S$ is the action of the configuration. The sum over fermion fields can be performed analytically, and one is left with a sum over the bosonic fields 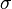$\sigma$ (which may have been originally part of the theory, or have been produced by a Hubbard-Stratonovich transformation to make the fermion action quadratic)

$Z = \int D \sigma \; \rho[\sigma]$

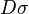where $D \sigma$ represents the measure for the sum over all configurations 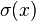$\sigma(x)$ of the bosonic fields, weighted by

$\rho[\sigma]=\det(M(\mu,\sigma))\exp(-S[\sigma])$

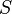where $S$ is now the action of the bosonic fields, and 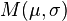$M(\mu,\sigma)$ is a matrix that encodes how the fermions were coupled to the bosons. The expectation value of an observable $A[\sigma]$ is therefore an average over all configurations weighted by $\rho[\sigma]$

$\langle A \rangle_\rho = \frac{\int D \sigma \; A[\sigma] \; \rho[\sigma]}{\int D \sigma \; \rho[\sigma]} .$

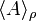If $\rho[\sigma]$ is positive, then it can be interpreted as a probability measure, and $\langle A \rangle_\rho$ can be calculated by performing the sum over field configurations numerically, using standard techniques such as Monte Carlo importance sampling.

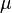The sign problem arises when $\rho[\sigma]$ is non-positive. This typically occurs in theories of fermions when the fermion chemical potential $\mu$ is nonzero, i.e. when there is a nonzero background density of fermions. If 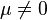$\mu\neq 0$ there is no particle-antiparticle symmetry, and 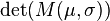$\det(M(\mu,\sigma))$, and hence the weight 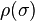$\rho(\sigma)$, is in general a complex number, so Monte-Carlo importance sampling cannot be used to evaluate the integral.

Reweighting procedure

A field theory with a non-positive weight can be transformed to one with a positive weight, by incorporating the non-positive part (sign or complex phase) of the weight into the observable. For example, one could decompose the weighting function into its modulus and phase,

$\rho[\sigma] = p[\sigma]\, \exp(i\theta[\sigma])$

where $p[\sigma]$ is real and positive, so

$\langle A \rangle_\rho = \frac{ \int D\sigma A[\sigma] \exp(i\theta[\sigma])\; p[\sigma]}{\int D\sigma \exp(i\theta[\sigma])\; p[\sigma]} = \frac{ \langle A[\sigma] \exp(i\theta[\sigma]) \rangle_p}{ \langle \exp(i\theta[\sigma]) \rangle_p}$

Note that the desired expectation value is now a ratio where the numerator and denominator are expectation values that both use a positive weighting function, $p[\sigma]$. However, the phase $\exp(i\theta[\sigma])$ is a highly oscillatory function in the configuration space, so if one uses Monte-Carlo methods to evaluate the numerator and denominator, each of them will evaluate to a very small number, whose exact value is swamped by the noise inherent in the Monte-Carlo sampling process. The "badness" of the sign problem is measured by the smallness of the denominator $\langle \exp(i\theta[\sigma]) \rangle_p$: if it is much less than 1 then the sign problem is severe. It can be shown (e.g.^[3]) that

$\langle \exp(i\theta[\sigma]) \rangle_p \propto \exp(-f V/T)$

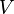where $V$ is the volume of the system, 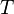$T$ is the temperature, and 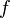$f$ is an energy density. The number of Monte-Carlo sampling points needed to obtain an accurate result therefore rises exponentially as the volume of the system becomes large, and as the temperature goes to zero.

The decomposition of the weighting function into modulus and phase is just one example (although it has been advocated as the optimal choice since it minimizes the variance of the denominator ^[4]). In general one could write

$\rho[\sigma] = p[\sigma] \frac{\rho[\sigma]}{p[\sigma]}$

where $p[\sigma]$ can be any positive weighting function (for example, the weighting function of the $\mu=0$ theory.)^[5] The badness of the sign problem is then measured by

$\left\langle \frac{\rho[\sigma]}{p[\sigma]}\right\rangle_p \propto \exp(-f V/T)$

which again goes to zero exponentially in the large-volume limit.

Methods for reducing the sign problem

The sign problem is NP-hard, implying that a full and generic solution of the sign problem would also solve all problems in the complexity class NP in polynomial time.^[6] If (as is generally suspected) there are no polynomial-time solutions to NP problems (see P versus NP problem), then there is no generic solution to the sign problem. This leaves open the possibility that there may be solutions that work in specific cases, where the oscillations of the integrand have a structure that can be exploited to reduce the numerical errors.

In systems with a moderate sign problem, such as field theories at a sufficiently high temperature or in a sufficiently small volume, the sign problem is not too severe and useful results can be obtained by various methods, such as more carefully tuned reweighting, analytic continuation from imaginary 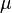$\mu$ to real 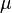$\mu$, or Taylor expansion in powers of 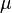$\mu$.^[2][7]

There are various proposals for solving systems with a severe sign problem:

• Meron-cluster algorithms. These achieve an exponential speed-up by decomposing the fermion world lines into clusters that contribute independently. Cluster algorithms have been developed for certain theories,^[3] but not for the Hubbard model of electrons, nor for QCD, the theory of quarks.
• Stochastic quantization. The sum over configurations is obtained as the equilibrium distribution of states explored by a complex Langevin equation. So far, the algorithm has been found to evade the sign problem in test models that have a sign problem but do not involve fermions.^[8]
• Fixed node method. One fixes the location of nodes (zeros) of the multiparticle wavefunction, and uses Monte-Carlo methods to obtain an estimate of the energy of the ground state, subject to that constraint.^[9]

References

1. E. Loh et al., "Sign problem in the numerical simulation of many-electron systems" Phys. Rev. B 41, 9301–9307 (1990)
2. O. Philipsen, "Lattice calculations at non-zero chemical potential: The QCD phase diagram", PoS Confinement8 011 (2008), Plenary talk at Quark Confinement and the Hadron Spectrum 8, Mainz, Germany, Sept 2008
3. S. Chandrasekharan and U.-J. Wiese, "Meron-Cluster Solution of Fermion Sign Problems", Phys. Rev. Lett. 83, 3116–3119 (1999) arXiv:cond-mat/9902128
4. T. D. Kieu and C. J. Griffin, "Monte Carlo simulations with indefinite and complex-valued measures", Phys. Rev. E 49, 3855–3859 (1994)
5. I. Barbour et al, "Results on finite density QCD", Nucl. Phys. Proc. Suppl. 60A 220-234 (1998), arXiv:hep-lat/9705042, presented at International Workshop on Lattice QCD on Parallel Computers, Tsukuba, Japan
6. M. Troyer, U.-J. Wiese, "Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations", Phys. Rev. Lett. 94, 170201 (2005), arXiv:cond-mat/0408370
7. C. Schmidt, "Lattice QCD at Finite Density", PoS LAT2006 021 (2006) arXiv:/hep-lat/0610116, plenary talk at 24th International Symposium on Lattice Field Theory.
8. G. Aarts, "Can stochastic quantization evade the sign problem? The relativistic Bose gas at finite chemical potential", Phys. Rev. Lett. 102, 131601 (2009), arXiv:0810.2089
9. H. J. M. van Bemmel et al, "Fixed-node quantum Monte Carlo method for lattice fermions", Phys. Rev. Lett. 72, 2442–2445 (1994)