Primitive cell

The parallelogram is the general primitive cell for the plane.

A parallelepiped is a general primitive cell for 3-dimensional space.

In geometry, crystallography, mineralogy, and solid state physics, a primitive cell is a minimum volume cell (a unit cell) corresponding to a single lattice point of a structure with discrete translational symmetry. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its primitive cell.

The primitive cell is a primitive unit. A primitive unit is a section of the tiling (usually a parallelogram or a set of neighboring tiles) that generates the whole tiling using only translations, and is as small as possible.

The primitive cell is a fundamental domain with respect to translational symmetry only. In the case of additional symmetries a fundamental domain is smaller.

The primitive translation vectors a→₁, a→₂, a→₃ span a lattice cell of smallest volume for a particular three-dimensional lattice, and are used to define a crystal translation vector

${\displaystyle {\vec {T}}=u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3}{\vec {a}}_{3},}$

where u₁, u₂, u₃ are integers, translation by which leaves the lattice invariant.^[1] That is, for a point in the lattice r, the arrangement of points appears the same from r′ = r + T→ as from r.^[2]

Since the primitive cell is defined by the primitive axes (vectors) a→₁, a→₂, a→₃, the volume V_p of the primitive cell is given by the parallelepiped from the above axes as

${\displaystyle V_{\mathrm {p} }=\left|{\vec {a}}_{1}\cdot ({\vec {a}}_{2}\times {\vec {a}}_{3})\right|.}$

A primitive cell is considered to contain exactly one lattice point. For unit cells generally, lattice points that are shared by n cells are counted as 1/n of the lattice points contained in each of those cells; so for example a primitive unit cell in three dimensions which has lattice points only at its eight vertices is considered to contain 1/8 of each of them.^[3]

A Wigner–Seitz cell is a primitive cell centered on the single lattice point it contains. This is a type of Voronoi cell. The Wigner–Seitz cell of the reciprocal lattice in momentum space is called the Brillouin zone.

2-dimensional primitive cell

A 2-dimensional primitive cell is a parallelogram, which in special cases may have orthogonal angles, or equal lengths, or both.

2-dimensional primitive cells

Parallelogram (Monoclinic)

Rhombus (Orthorhombic)

Rectangle (Orthorhombic)

Square (Tetragonal)

3-dimensional primitive cell

A crystal can be categorized by its lattice and the atoms that lie in a primitive cell (the basis). A cell will fill all the lattice space without leaving gaps by repetition of crystal translation operations.

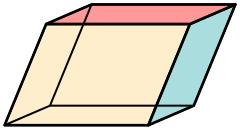
A 3-dimensional primitive cell is a parallelepiped, which in special cases may have orthogonal angles, or equal lengths, or both.

3-dimensional primitive cells

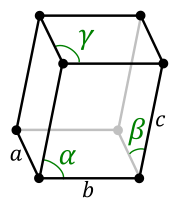Parallelepiped (Triclinic)

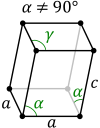Clinorhombic prism (Monoclinic)

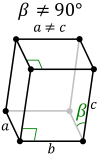Right parallelogrammic prism (Monoclinic)

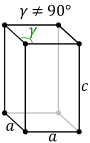Right rhombic prism (Orthorhombic)

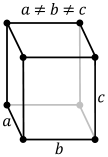Rectangular cuboid (Orthorhombic)

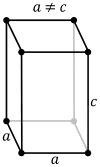Square cuboid (Tetragonal)

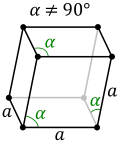Trigonal trapezohedron (Rhombohedral)

Cube (Cubic)

See also

• Wigner–Seitz cell
• Bravais lattice
• Wallpaper group
• Space group

Notes

1. In n dimensions the crystal translation vector would be

   ${\displaystyle {\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.}$

2. Kittel, Charles (2004). Introduction to Solid State Physics (8th ed.). p. 4.
3. "DoITPoMS - TLP Library Crystallography - Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.