Spherical pendulum

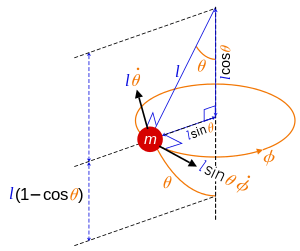
Spherical pendulum: angles and velocities.

In physics, a spherical pendulum is a higher dimensional analogue of the pendulum. It consists of a mass m moving without friction on the surface of a sphere. The only forces acting on the mass are the reaction from the sphere and gravity.

Owing to the spherical geometry of the problem, spherical coordinates are used to describe the position of the mass in terms of (r, θ, φ), where r is fixed. In what follows l is the constant length of the pendulum, so r = l.

Lagrangian mechanics

The Lagrangian is ^[1]

$L={\frac {1}{2}}mr^{2}\left({\dot {\theta }}^{2}+\sin ^{2}\theta \ {\dot {\phi }}^{2}\right)+mgr\cos \theta .$

The Euler–Lagrange equations give :

${\frac {d}{dt}}\left(mr^{2}{\dot {\theta }}\right)-mr^{2}\sin \theta \cos \theta {\dot {\phi }}^{2}+mgr\sin \theta =0$

and

${\frac {d}{dt}}\left(mr^{2}\sin ^{2}\theta \,{\dot {\phi }}\right)=0$

showing that angular momentum is conserved.

Hamiltonian mechanics

The Hamiltonian is

$H=P_{\theta }{\dot {\theta }}+P_{\phi }{\dot {\phi }}-L$

where

$P_{\theta }={\frac {\partial L}{\partial {\dot {\theta }}}}=mr^{2}{\dot {\theta }}$

and

$P_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}}=mr^{2}{\dot {\phi }}\sin ^{2}\theta$

See also

• Conical Pendulum
• Newton's three laws of motion
• Pendulum
• Pendulum (mathematics)
• Routhian mechanics

References

1. Landau, Lev Davidovich; Evgenii Mikhailovich Lifshitz (1976). Course of Theoretical Physics: Volume 1 Mechanics. Butterworth-Heinenann. pp. 33–34. ISBN 0750628960.