Splitter (geometry)
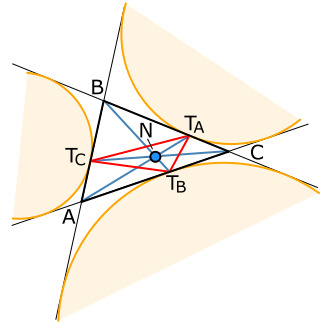
In plane geometry, a splitter is a line segment through one of the vertices of a triangle (that is, a cevian) that bisects the perimeter of the triangle.[1][2]
Properties
The opposite endpoint of a splitter to the chosen triangle vertex lies at the point on the triangle's side where one of the excircles of the triangle is tangent to that side.[1][2] This point is also called a splitting point of the triangle.[2] It is additionally a vertex of the extouch triangle and one of the points where the Mandart inellipse is tangent to the triangle side.[3]
The three splitters concur at the Nagel point of the triangle,[1] which is also called its splitting center.[2]
Generalization
Some authors have used the term "splitter" in a more general sense, for any line segment that bisects the perimeter of the triangle. Other line segments of this type include the cleavers, which are perimeter-bisecting segments that pass through the midpoint of a triangle side, and the equalizers, segments that bisect both the area and perimeter of a triangle.[4]
References
- 1 2 3 Honsberger, Ross (1995), "Chapter 1: Cleavers and Splitters", Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Mathematical Association of America, pp. 1–14.
- 1 2 3 4 Avishalom, Dov (1963), "The perimetric bisection of triangles", Mathematics Magazine, 36 (1): 60–62, JSTOR 2688140, MR 1571272.
- ↑ Juhász, Imre (2012), "Control point based representation of inellipses of triangles" (PDF), Annales Mathematicae et Informaticae, 40: 37–46, MR 3005114.
- ↑ Kodokostas, Dimitrios (2010), "Triangle equalizers", Mathematics Magazine, 83 (2): 141–146, doi:10.4169/002557010X482916.