Uncertainty theory

Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms. It was founded by Baoding Liu ^[1] in 2007 and refined in 2009.^[2]

Mathematical measures of the likelihood of an event being true include probability theory, capacity, fuzzy logic, possibility, and credibility, as well as uncertainty.

Five axioms

Axiom 1. (Normality Axiom) ${\displaystyle {\mathcal {M}}\{\Gamma \}=1{\text{ for the universal set }}\Gamma }$.

Axiom 2. (Monotonicity Axiom) ${\displaystyle {\mathcal {M}}\{\Lambda _{1}\}\leq {\mathcal {M}}\{\Lambda _{2}\}{\text{ whenever }}\Lambda _{1}\subset \Lambda _{2}}$.

Axiom 3. (Self-Duality Axiom) ${\displaystyle {\mathcal {M}}\{\Lambda \}+{\mathcal {M}}\{\Lambda ^{c}\}=1{\text{ for any event }}\Lambda }$.

Axiom 4. (Countable Subadditivity Axiom) For every countable sequence of events Λ₁, Λ₂, ..., we have

${\displaystyle {\mathcal {M}}\left\{\bigcup _{i=1}^{\infty }\Lambda _{i}\right\}\leq \sum _{i=1}^{\infty }{\mathcal {M}}\{\Lambda _{i}\}}$.

Axiom 5. (Product Measure Axiom) Let ${\displaystyle (\Gamma _{k},{\mathcal {L}}_{k},{\mathcal {M}}_{k})}$ be uncertainty spaces for ${\displaystyle k=1,2,\cdots ,n}$. Then the product uncertain measure ${\mathcal {M}}$ is an uncertain measure on the product σ-algebra satisfying

${\displaystyle {\mathcal {M}}\left\{\prod _{i=1}^{n}\Lambda _{i}\right\}={\underset {1\leq i\leq n}{\operatorname {min} }}{\mathcal {M}}_{i}\{\Lambda _{i}\}}$.

Principle. (Maximum Uncertainty Principle) For any event, if there are multiple reasonable values that an uncertain measure may take, then the value as close to 0.5 as possible is assigned to the event.

Uncertain variables

An uncertain variable is a measurable function ξ from an uncertainty space ${\displaystyle (\Gamma ,L,M)}$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set ${\displaystyle \{\xi \in B\}=\{\gamma \in \Gamma |\xi (\gamma )\in B\}}$ is an event.

Uncertainty distribution

Uncertainty distribution is inducted to describe uncertain variables.

Definition:The uncertainty distribution ${\displaystyle \Phi (x):R\rightarrow [0,1]}$ of an uncertain variable ξ is defined by ${\displaystyle \Phi (x)=M\{\xi \leq x\}}$.

Theorem(Peng and Iwamura, Sufficient and Necessary Condition for Uncertainty Distribution) A function ${\displaystyle \Phi (x):R\rightarrow [0,1]}$ is an uncertain distribution if and only if it is an increasing function except ${\displaystyle \Phi (x)\equiv 0}$ and ${\displaystyle \Phi (x)\equiv 1}$.

Independence

Definition: The uncertain variables ${\displaystyle \xi _{1},\xi _{2},\ldots ,\xi _{m}}$ are said to be independent if

${\displaystyle M\{\cap _{i=1}^{m}(\xi \in B_{i})\}={\mbox{min}}_{1\leq i\leq m}M\{\xi _{i}\in B_{i}\}}$

for any Borel sets ${\displaystyle B_{1},B_{2},\ldots ,B_{m}}$ of real numbers.

Theorem 1: The uncertain variables ${\displaystyle \xi _{1},\xi _{2},\ldots ,\xi _{m}}$ are independent if

${\displaystyle M\{\cup _{i=1}^{m}(\xi \in B_{i})\}={\mbox{max}}_{1\leq i\leq m}M\{\xi _{i}\in B_{i}\}}$

for any Borel sets ${\displaystyle B_{1},B_{2},\ldots ,B_{m}}$ of real numbers.

Theorem 2: Let ${\displaystyle \xi _{1},\xi _{2},\ldots ,\xi _{m}}$ be independent uncertain variables, and ${\displaystyle f_{1},f_{2},\ldots ,f_{m}}$ measurable functions. Then ${\displaystyle f_{1}(\xi _{1}),f_{2}(\xi _{2}),\ldots ,f_{m}(\xi _{m})}$ are independent uncertain variables.

Theorem 3: Let $\Phi _{i}$ be uncertainty distributions of independent uncertain variables ${\displaystyle \xi _{i},\quad i=1,2,\ldots ,m}$ respectively, and $\Phi$ the joint uncertainty distribution of uncertain vector ${\displaystyle (\xi _{1},\xi _{2},\ldots ,\xi _{m})}$. If ${\displaystyle \xi _{1},\xi _{2},\ldots ,\xi _{m}}$ are independent, then we have

${\displaystyle \Phi (x_{1},x_{2},\ldots ,x_{m})={\mbox{min}}_{1\leq i\leq m}\Phi _{i}(x_{i})}$

for any real numbers $x_{1},x_{2},\ldots ,x_{m}$.

Operational law

Theorem: Let ${\displaystyle \xi _{1},\xi _{2},\ldots ,\xi _{m}}$ be independent uncertain variables, and ${\displaystyle f:R^{n}\rightarrow R}$ a measurable function. Then ${\displaystyle \xi =f(\xi _{1},\xi _{2},\ldots ,\xi _{m})}$ is an uncertain variable such that

${\displaystyle {\mathcal {M}}\{\xi \in B\}={\begin{cases}{\underset {f(B_{1},B_{2},\cdots ,B_{n})\subset B}{\operatorname {sup} }}\;{\underset {1\leq k\leq n}{\operatorname {min} }}{\mathcal {M}}_{k}\{\xi _{k}\in B_{k}\},&{\text{if }}{\underset {f(B_{1},B_{2},\cdots ,B_{n})\subset B}{\operatorname {sup} }}\;{\underset {1\leq k\leq n}{\operatorname {min} }}{\mathcal {M}}_{k}\{\xi _{k}\in B_{k}\}>0.5\\1-{\underset {f(B_{1},B_{2},\cdots ,B_{n})\subset B^{c}}{\operatorname {sup} }}\;{\underset {1\leq k\leq n}{\operatorname {min} }}{\mathcal {M}}_{k}\{\xi _{k}\in B_{k}\},&{\text{if }}{\underset {f(B_{1},B_{2},\cdots ,B_{n})\subset B^{c}}{\operatorname {sup} }}\;{\underset {1\leq k\leq n}{\operatorname {min} }}{\mathcal {M}}_{k}\{\xi _{k}\in B_{k}\}>0.5\\0.5,&{\text{otherwise}}\end{cases}}}$

where ${\displaystyle B,B_{1},B_{2},\ldots ,B_{m}}$ are Borel sets, and ${\displaystyle f(B_{1},B_{2},\ldots ,B_{m})\subset B}$ means${\displaystyle f(x_{1},x_{2},\ldots ,x_{m})\in B}$ for any${\displaystyle x_{1}\in B_{1},x_{2}\in B_{2},\ldots ,x_{m}\in B_{m}}$.

Expected Value

Definition: Let $\xi$ be an uncertain variable. Then the expected value of $\xi$ is defined by

${\displaystyle E[\xi ]=\int _{0}^{+\infty }M\{\xi \geq r\}dr-\int _{-\infty }^{0}M\{\xi \leq r\}dr}$

provided that at least one of the two integrals is finite.

Theorem 1: Let $\xi$ be an uncertain variable with uncertainty distribution $\Phi$. If the expected value exists, then

${\displaystyle E[\xi ]=\int _{0}^{+\infty }(1-\Phi (x))dx-\int _{-\infty }^{0}\Phi (x)dx}$.

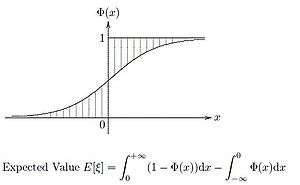
Theorem 2: Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi$. If the expected value exists, then

${\displaystyle E[\xi ]=\int _{0}^{1}\Phi ^{-1}(\alpha )d\alpha }$.

Theorem 3: Let $\xi$ and $\eta$ be independent uncertain variables with finite expected values. Then for any real numbers $a$ and $b$, we have

${\displaystyle E[a\xi +b\eta ]=aE[\xi ]+b[\eta ]}$.

Variance

Definition: Let $\xi$ be an uncertain variable with finite expected value $e$. Then the variance of $\xi$ is defined by

${\displaystyle V[\xi ]=E[(\xi -e)^{2}]}$.

Theorem: If $\xi$ be an uncertain variable with finite expected value, $a$ and $b$ are real numbers, then

${\displaystyle V[a\xi +b]=a^{2}V[\xi ]}$.

Critical value

Definition: Let $\xi$ be an uncertain variable, and ${\displaystyle \alpha \in (0,1]}$. Then

${\displaystyle \xi _{sup}(\alpha )={\mbox{sup}}\{r|M\{\xi \geq r\}\geq \alpha \}}$

is called the α-optimistic value to $\xi$, and

${\displaystyle \xi _{inf}(\alpha )={\mbox{inf}}\{r|M\{\xi \leq r\}\geq \alpha \}}$

is called the α-pessimistic value to $\xi$.

Theorem 1: Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi$. Then its α-optimistic value and α-pessimistic value are

${\displaystyle \xi _{sup}(\alpha )=\Phi ^{-1}(1-\alpha )}$,

${\displaystyle \xi _{inf}(\alpha )=\Phi ^{-1}(\alpha )}$.

Theorem 2: Let $\xi$ be an uncertain variable, and ${\displaystyle \alpha \in (0,1]}$. Then we have

• if ${\displaystyle \alpha >0.5}$, then ${\displaystyle \xi _{inf}(\alpha )\geq \xi _{sup}(\alpha )}$;
• if ${\displaystyle \alpha \leq 0.5}$, then ${\displaystyle \xi _{inf}(\alpha )\leq \xi _{sup}(\alpha )}$.

Theorem 3: Suppose that $\xi$ and $\eta$ are independent uncertain variables, and ${\displaystyle \alpha \in (0,1]}$. Then we have

${\displaystyle (\xi +\eta )_{sup}(\alpha )=\xi _{sup}(\alpha )+\eta _{sup}{\alpha }}$,

${\displaystyle (\xi +\eta )_{inf}(\alpha )=\xi _{inf}(\alpha )+\eta _{inf}{\alpha }}$,

${\displaystyle (\xi \vee \eta )_{sup}(\alpha )=\xi _{sup}(\alpha )\vee \eta _{sup}{\alpha }}$,

${\displaystyle (\xi \vee \eta )_{inf}(\alpha )=\xi _{inf}(\alpha )\vee \eta _{inf}{\alpha }}$,

${\displaystyle (\xi \wedge \eta )_{sup}(\alpha )=\xi _{sup}(\alpha )\wedge \eta _{sup}{\alpha }}$,

${\displaystyle (\xi \wedge \eta )_{inf}(\alpha )=\xi _{inf}(\alpha )\wedge \eta _{inf}{\alpha }}$.

Entropy

Definition: Let $\xi$ be an uncertain variable with uncertainty distribution $\Phi$. Then its entropy is defined by

${\displaystyle H[\xi ]=\int _{-\infty }^{+\infty }S(\Phi (x))dx}$

where ${\displaystyle S(x)=-t{\mbox{ln}}(t)-(1-t){\mbox{ln}}(1-t)}$.

Theorem 1(Dai and Chen): Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi$. Then

${\displaystyle H[\xi ]=\int _{0}^{1}\Phi ^{-1}(\alpha ){\mbox{ln}}{\frac {\alpha }{1-\alpha }}d\alpha }$.

Theorem 2: Let $\xi$ and $\eta$ be independent uncertain variables. Then for any real numbers $a$ and $b$, we have

${\displaystyle H[a\xi +b\eta ]=|a|E[\xi ]+|b|E[\eta ]}$.

Theorem 3: Let $\xi$ be an uncertain variable whose uncertainty distribution is arbitrary but the expected value $e$ and variance $\sigma ^{2}$. Then

${\displaystyle H[\xi ]\leq {\frac {\pi \sigma }{\sqrt {3}}}}$.

Inequalities

Theorem 1(Liu, Markov Inequality): Let $\xi$ be an uncertain variable. Then for any given numbers $t > 0$ and $p>0$, we have

${\displaystyle M\{|\xi |\geq t\}\leq {\frac {E[|\xi |^{p}]}{t^{p}}}}$.

Theorem 2 (Liu, Chebyshev Inequality) Let $\xi$ be an uncertain variable whose variance ${\displaystyle V[\xi ]}$ exists. Then for any given number${\displaystyle t>0}$, we have

${\displaystyle M\{|\xi -E[\xi ]|\geq t\}\leq {\frac {V[\xi ]}{t^{2}}}}$.

Theorem 3 (Liu, Holder’s Inequality) Let $p$ and $q$ be positive numbers with $1/p+1/q=1$, and let $\xi$ and $\eta$ be independent uncertain variables with ${\displaystyle E[|\xi |^{p}]<\infty }$ and ${\displaystyle E[|\eta |^{q}]<\infty }$. Then we have

${\displaystyle E[|\xi \eta |]\leq {\sqrt[{p}]{E[|\xi |^{p}]}}{\sqrt[{p}]{E[\eta |^{p}]}}}$.

Theorem 4:(Liu [127], Minkowski Inequality) Let $p$ be a real number with ${\displaystyle p\leq 1}$, and let $\xi$ and $\eta$ be independent uncertain variables with ${\displaystyle E[|\xi |^{p}]<\infty }$ and ${\displaystyle E[|\eta |^{q}]<\infty }$. Then we have

${\displaystyle {\sqrt[{p}]{E[|\xi +\eta |^{p}]}}\leq {\sqrt[{p}]{E[|\xi |^{p}]}}+{\sqrt[{p}]{E[\eta |^{p}]}}}$.

Convergence concept

Definition 1: Suppose that ${\displaystyle \xi ,\xi _{1},\xi _{2},\ldots }$ are uncertain variables defined on the uncertainty space ${\displaystyle (\Gamma ,L,M)}$. The sequence ${\displaystyle \{\xi _{i}\}}$ is said to be convergent a.s. to $\xi$ if there exists an event $\Lambda$ with ${\displaystyle M\{\Lambda \}=1}$ such that

${\displaystyle {\mbox{lim}}_{i\rightarrow \infty }|\xi _{i}(\gamma )-\xi (\gamma )|=0}$

for every ${\displaystyle \gamma \in \Lambda }$. In that case we write ${\displaystyle \xi _{i}\rightarrow \xi }$,a.s.

Definition 2: Suppose that ${\displaystyle \xi ,\xi _{1},\xi _{2},\ldots }$ are uncertain variables. We say that the sequence ${\displaystyle \{\xi _{i}\}}$ converges in measure to $\xi$ if

${\displaystyle {\mbox{lim}}_{i\rightarrow \infty }M\{|\xi _{i}-\xi |\leq \varepsilon \}=0}$

for every $\varepsilon >0$.

Definition 3: Suppose that ${\displaystyle \xi ,\xi _{1},\xi _{2},\ldots }$ are uncertain variables with finite expected values. We say that the sequence ${\displaystyle \{\xi _{i}\}}$ converges in mean to $\xi$ if

${\displaystyle {\mbox{lim}}_{i\rightarrow \infty }E[|\xi _{i}-\xi |]=0}$.

Definition 4: Suppose that ${\displaystyle \Phi ,\phi _{1},\Phi _{2},\ldots }$ are uncertainty distributions of uncertain variables ${\displaystyle \xi ,\xi _{1},\xi _{2},\ldots }$, respectively. We say that the sequence ${\displaystyle \{\xi _{i}\}}$ converges in distribution to $\xi$ if ${\displaystyle \Phi _{i}\rightarrow \Phi }$ at any continuity point of $\Phi$.

Theorem 1: Convergence in Mean $\Rightarrow$ Convergence in Measure $\Rightarrow$ Convergence in Distribution. However, Convergence in Mean $\nLeftrightarrow$ Convergence Almost Surely $\nLeftrightarrow$ Convergence in Distribution.

Conditional uncertainty

Definition 1: Let ${\displaystyle (\Gamma ,L,M)}$ be an uncertainty space, and ${\displaystyle A,B\in L}$. Then the conditional uncertain measure of A given B is defined by

${\displaystyle {\mathcal {M}}\{A\vert B\}={\begin{cases}\displaystyle {\frac {{\mathcal {M}}\{A\cap B\}}{{\mathcal {M}}\{B\}}},&\displaystyle {\text{if }}{\frac {{\mathcal {M}}\{A\cap B\}}{{\mathcal {M}}\{B\}}}<0.5\\\displaystyle 1-{\frac {{\mathcal {M}}\{A^{c}\cap B\}}{{\mathcal {M}}\{B\}}},&\displaystyle {\text{if }}{\frac {{\mathcal {M}}\{A^{c}\cap B\}}{{\mathcal {M}}\{B\}}}<0.5\\0.5,&{\text{otherwise}}\end{cases}}}$

${\displaystyle {\text{provided that }}{\mathcal {M}}\{B\}>0}$

Theorem 1: Let ${\displaystyle (\Gamma ,L,M)}$ be an uncertainty space, and B an event with ${\displaystyle M\{B\}>0}$. Then M{·|B} defined by Definition 1 is an uncertain measure, and ${\displaystyle (\Gamma ,L,M\{{\mbox{·}}|B\})}$is an uncertainty space.

Definition 2: Let $\xi$ be an uncertain variable on ${\displaystyle (\Gamma ,L,M)}$. A conditional uncertain variable of $\xi$ given B is a measurable function ${\displaystyle \xi |_{B}}$ from the conditional uncertainty space ${\displaystyle (\Gamma ,L,M\{{\mbox{·}}|_{B}\})}$ to the set of real numbers such that

${\displaystyle \xi |_{B}(\gamma )=\xi (\gamma ),\forall \gamma \in \Gamma }$.

Definition 3: The conditional uncertainty distribution ${\displaystyle \Phi \rightarrow [0,1]}$ of an uncertain variable $\xi$ given B is defined by

${\displaystyle \Phi (x|B)=M\{\xi \leq x|B\}}$

provided that ${\displaystyle M\{B\}>0}$.

Theorem 2: Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi (x)$, and $t$ a real number with ${\displaystyle \Phi (t)<1}$. Then the conditional uncertainty distribution of $\xi$ given ${\displaystyle \xi >t}$ is

${\displaystyle \Phi (x\vert (t,+\infty ))={\begin{cases}0,&{\text{if }}\Phi (x)\leq \Phi (t)\\\displaystyle {\frac {\Phi (x)}{1-\Phi (t)}}\land 0.5,&{\text{if }}\Phi (t)<\Phi (x)\leq (1+\Phi (t))/2\\\displaystyle {\frac {\Phi (x)-\Phi (t)}{1-\Phi (t)}},&{\text{if }}(1+\Phi (t))/2\leq \Phi (x)\end{cases}}}$

Theorem 3: Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi (x)$, and $t$ a real number with ${\displaystyle \Phi (t)>0}$. Then the conditional uncertainty distribution of $\xi$ given ${\displaystyle \xi \leq t}$ is

${\displaystyle \Phi (x\vert (-\infty ,t])={\begin{cases}\displaystyle {\frac {\Phi (x)}{\Phi (t)}},&{\text{if }}\Phi (x)\leq \Phi (t)/2\\\displaystyle {\frac {\Phi (x)+\Phi (t)-1}{\Phi (t)}}\lor 0.5,&{\text{if }}\Phi (t)/2\leq \Phi (x)<\Phi (t)\\1,&{\text{if }}\Phi (t)\leq \Phi (x)\end{cases}}}$

Definition 4: Let $\xi$ be an uncertain variable. Then the conditional expected value of $\xi$ given B is defined by

${\displaystyle E[\xi |B]=\int _{0}^{+\infty }M\{\xi \geq r|B\}dr-\int _{-\infty }^{0}M\{\xi \leq r|B\}dr}$

provided that at least one of the two integrals is finite.

References

1. Baoding Liu, Uncertainty Theory, 2nd ed., Springer-Verlag, Berlin, 2007.
2. Baoding Liu, Uncertainty Theory, 4th ed., http://orsc.edu.cn/liu/ut.pdf.

• Xin Gao, Some Properties of Continuous Uncertain Measure, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol.17, No.3, 419-426, 2009.
• Cuilian You, Some Convergence Theorems of Uncertain Sequences, Mathematical and Computer Modelling, Vol.49, Nos.3-4, 482-487, 2009.
• Yuhan Liu, How to Generate Uncertain Measures, Proceedings of Tenth National Youth Conference on Information and Management Sciences, August 3–7, 2008, Luoyang, pp. 23–26.
• Baoding Liu, Some Research Problems in Uncertainty Theory, Journal of Uncertain Systems, Vol.3, No.1, 3-10, 2009.
• Yang Zuo, Xiaoyu Ji, Theoretical Foundation of Uncertain Dominance, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 827–832.
• Yuhan Liu and Minghu Ha, Expected Value of Function of Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 779–781.
• Zhongfeng Qin, On Lognormal Uncertain Variable, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 753–755.
• Jin Peng, Value at Risk and Tail Value at Risk in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 787–793.
• Yi Peng, U-Curve and U-Coefficient in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 815–820.
• Wei Liu, Jiuping Xu, Some Properties on Expected Value Operator for Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 808–811.
• Xiaohu Yang, Moments and Tails Inequality within the Framework of Uncertainty Theory, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 812–814.
• Yuan Gao, Analysis of k-out-of-n System with Uncertain Lifetimes, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 794–797.
• Xin Gao, Shuzhen Sun, Variance Formula for Trapezoidal Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 853–855.
• Zixiong Peng, A Sufficient and Necessary Condition of Product Uncertain Null Set, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 798–801.