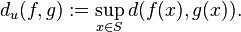Uniformly Cauchy sequence

In mathematics, a sequence of functions 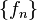$\{f_{n}\}$ from a set S to a metric space M is said to be uniformly Cauchy if:

• For all 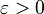$\varepsilon > 0$, there exists 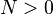$N>0$ such that for all 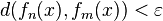$x\in S$: $d(f_{n}(x), f_{m}(x)) < \varepsilon$ whenever $m, n > N$.

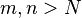Another way of saying this is that 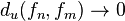$d_u (f_{n}, f_{m}) \to 0$ as $m, n \to \infty$, where the uniform distance $d_u$ between two functions is defined by

$d_{u} (f, g) := \sup_{x \in S} d (f(x), g(x)).$

Convergence criteria

A sequence of functions {f_n} from S to M is pointwise Cauchy if, for each x ∈ S, the sequence {f_n(x)} is a Cauchy sequence in M. This is a weaker condition than being uniformly Cauchy.

In general a sequence can be pointwise Cauchy and not pointwise convergent, or it can be uniformly Cauchy and not uniformly convergent. Nevertheless, if the metric space M is complete, then any pointwise Cauchy sequence converges pointwise to a function from S to M. Similarly, any uniformly Cauchy sequence will tend uniformly to such a function.

The uniform Cauchy property is frequently used when the S is not just a set, but a topological space, and M is a complete metric space. The following theorem holds:

• Let S be a topological space and M a complete metric space. Then any uniformly Cauchy sequence of continuous functions f_n : S → M tends uniformly to a unique continuous function f : S → M.

Generalization to uniform spaces

A sequence of functions 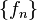$\{f_{n}\}$ from a set S to a metric space U is said to be uniformly Cauchy if:

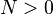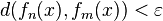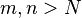• For all $x\in S$ and for any entourage $\varepsilon$, there exists $N>0$ such that $d(f_{n}(x), f_{m}(x)) < \varepsilon$ whenever $m, n > N$.

See also

• Modes of convergence (annotated index)